题目内容
17.过椭圆$\frac{{x}^{2}}{2}$+y2=1上的一个动点P向x轴引垂线交于M,延长MP到N(P在MN中间)使$\overrightarrow{MP}$=λ$\overrightarrow{MN}$(λ>0,λ≠1),所得N点轨迹与椭圆有相同的离心率,则λ=$\frac{1}{2}$.分析 确定N点的轨迹方程为$\frac{{x}^{2}}{2}$+λ2y2=1,利用N点轨迹与椭圆有相同的离心率,建立方程,即可求出λ.
解答 解:设N(x,y),P(x,y0),M(x,0),所以(0,y0)=λ(0,y),则y0=λy,
∴N点的轨迹方程为$\frac{{x}^{2}}{2}$+λ2y2=1,
∵λ>0,λ≠1,
故轨迹是焦点在y轴上的椭圆,
∴$\frac{\sqrt{2}}{2}$=$\sqrt{\frac{\frac{1}{{λ}^{2}}-2}{\frac{1}{{λ}^{2}}}}$,
∴λ=$\frac{1}{2}$.
故答案为:$\frac{1}{2}$.
点评 本题考查轨迹方程,考查椭圆的性质,考查学生的计算能力,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
5.下列四个函数:①y=$\frac{x}{x-1}$;②y=x2+x;③y=-(x+1)2;④y=$\frac{x}{1-x}$+2,其中在(-∞,0)上为减函数的是( )
| A. | ① | B. | ④ | C. | ①④ | D. | ①②④ |
8.曲线${∫}_{-\sqrt{2}}^{2}$(-$\sqrt{2-{x}^{2}}$)dx( )
| A. | -2π | B. | -π | C. | 2π | D. | π |
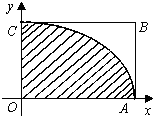 如图,曲线AC的方程为$\frac{x^2}{9}+\frac{y^2}{4}$═1(0≤x≤3,0≤y≤2),为估计椭圆$\frac{x^2}{9}+\frac{y^2}{4}$═1的面积,现采用随机模拟方式产生x∈(0,3),y∈(0,2)的200个点(x,y),经统计,落在图中阴影部分的点共157个,则可估计椭圆$\frac{x^2}{9}+\frac{y^2}{4}$═1的面积是18.84.(精确到0.01)
如图,曲线AC的方程为$\frac{x^2}{9}+\frac{y^2}{4}$═1(0≤x≤3,0≤y≤2),为估计椭圆$\frac{x^2}{9}+\frac{y^2}{4}$═1的面积,现采用随机模拟方式产生x∈(0,3),y∈(0,2)的200个点(x,y),经统计,落在图中阴影部分的点共157个,则可估计椭圆$\frac{x^2}{9}+\frac{y^2}{4}$═1的面积是18.84.(精确到0.01) 如图所示,四棱锥P-ABCD的底面是一梯形,AB∥CD,CD=3AB,过点B作平面PAD的平行线交直线PC于点E,则点PE:EC=1:2.
如图所示,四棱锥P-ABCD的底面是一梯形,AB∥CD,CD=3AB,过点B作平面PAD的平行线交直线PC于点E,则点PE:EC=1:2.