题目内容
7．
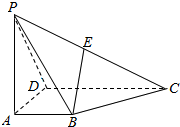如图所示，四棱锥P-ABCD的底面是一梯形，AB∥CD，CD=3AB，过点B作平面PAD的平行线交直线PC于点E，则点PE：EC=1：2．
分析 利用过点B作平面PAD的平行线，推出直线与平面平行，利用判定定理推出E的位置，然后求解比例大小．
解答 解：取PD的3等分点F，PE=$\frac{1}{2}$EC，连接EF，AF，AB∥CD，CD=3AB，
所以EF∥AB，且EF=$\frac{1}{3}$CD，又AB∥CD，CD=3AB，
EF=AB，从而四边形ABEF为平行四边形，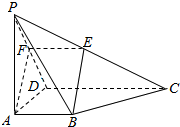
所以，BE∥AF，BE?平面PAD，AF?平面PAD，
根据线面平行的判定定理可得BE∥平面PAD；
所以PE：EC=1：2．
故答案为：1：2．
点评 本题考查线面平行的判定，要注意转化思想的应用，即将线面平行转化为线线平行或者面面平行进行证明．
练习册系列答案
相关题目
18．已知双曲线$\frac{x^2}{12}-\frac{y^2}{4}=1$的右焦点为F，若过点F的直线与双曲线的右支有且只有一个交点，则此直线的斜率的取值范围是（ ）
| A． | $[{-\frac{{\sqrt{3}}}{3}，\frac{{\sqrt{3}}}{3}}]$ | B． | $\left?{-\sqrt{3}，\sqrt{3}}\right?$ | C． | $（{-\frac{{\sqrt{3}}}{3}，\frac{{\sqrt{3}}}{3}}）$ | D． | $（{-\sqrt{3}，\sqrt{3}}）$ |
15．在直三棱柱A1B1C1-ABC中，$∠BAC=\frac{π}{2}$，AB=AC=AA1=1，已知G和E分别为A1B1和CC1的中点，D与F分别为线段AC和AB上的动点（不包括端点），若GD⊥EF，则线段DF的长度的取值范围为（ ）
| A． | [$\frac{\sqrt{5}}{5}$，1） | B． | [$\frac{\sqrt{5}}{5}$，1] | C． | （$\frac{2\sqrt{5}}{5}$，1） | D． | [$\frac{2\sqrt{5}}{5}$，1） |