题目内容
已知三棱柱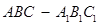 的侧棱与底面边长都相等,
的侧棱与底面边长都相等,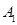 在底面
在底面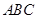 内的射影为
内的射影为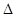
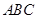 的中心,则
的中心,则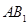 与底面
与底面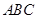 所成角的正弦值等于( )
所成角的正弦值等于( )
A. | B.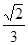 | C.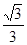 | D.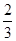 |
B
解析试题分析:根据题意可知,ABC的中心为O,连CO并延长交AB于D,过B1作B1E⊥AB交AB的延长线于E,再过B1作B1F⊥平面ABC交平面ABC于F。
设AB=a。∵AB=AC=BC=a,O是△ABC的中心,∴CD⊥AD、AD=BD= ,∴CD=
,∴CD=
显然有:  。
。
∵O是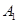 在平面ABC上的射影,∴
在平面ABC上的射影,∴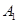 O⊥平面ABC,∴AD⊥
O⊥平面ABC,∴AD⊥ ,又AD⊥CD、CD∩
,又AD⊥CD、CD∩ =O,∴AD⊥平面
=O,∴AD⊥平面 ,∴AD⊥
,∴AD⊥ 。
。
由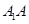 =a、AD=
=a、AD= 、
、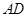 ⊥
⊥ ,得:
,得: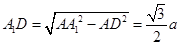 。∵
。∵ ⊥平面ABC,∴
⊥平面ABC,∴ ⊥
⊥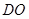
由 、
、 、
、 ⊥
⊥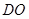 ,得:
,得: =
=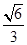
∵ ⊥
⊥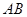 、
、 ⊥
⊥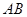 ,∴
,∴ ∥
∥
∵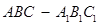 是三棱柱,∴
是三棱柱,∴ 。
。
由 ∥
∥ ,
, 得:
得: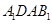 是平行四边形,∴
是平行四边形,∴ =
= 、
、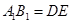 =a显然,有:AE=AD+DE=
=a显然,有:AE=AD+DE= +a=
+a= 。
。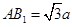
∵ ⊥平面ABC,
⊥平面ABC,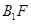 ⊥平面ABC,∴
⊥平面ABC,∴ ∥
∥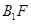 ,∴
,∴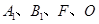 共面。
共面。
∵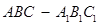 是三棱柱,∴
是三棱柱,∴ ∥平面ABC,而平面ABC∩平面
∥平面ABC,而平面ABC∩平面 =OF,∴
=OF,∴ ∥OF。由
∥OF。由 ∥
∥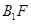 、
、 ∥OF,得:
∥OF,得: 是平行四边形,∴
是平行四边形,∴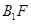 =
= =
=
∵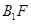 ⊥平面ABC,∴
⊥平面ABC,∴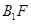 ⊥AF。,得:sin∠
⊥AF。,得:sin∠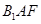 =
=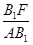 =
=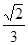
考点:本试题考查了线面角的求解知识。
点评:对于该试题中的线面角的求解,关键是建立线面垂直的背景,同时根据已知的边长和侧棱长的关系式得到角度,进而求解运算,属于难度试题。

练习册系列答案
相关题目
在空间,下列命题正确的是( )
| A.平行直线在同一平面内的射影平行或重合 | B.垂直于同一平面的两条直线平行 |
| C.垂直于同一平面的两个平面平行 | D.平行于同一直线的两个平面平行 |
在正方体 中,直线
中,直线 与平面
与平面 所成的角的大小为( )
所成的角的大小为( )
| A.900 | B.600 | C.450 | D.300 |
已知 、
、 是两条不同的直线,
是两条不同的直线, 、
、 是两个不同的平面,则下列命题中正确的是
是两个不同的平面,则下列命题中正确的是
A.若 ,且 ,且 ,则 ,则 |
B.若 ,且 ,且 ,则 ,则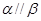 |
C.若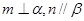 ,且 ,且 ,则 ,则 |
D.若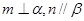 ,且 ,且 ,则 ,则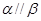 |
设a、b是两条不重合的直线,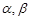 是两个不重合的平面,则下列命题中不正确的一个是
是两个不重合的平面,则下列命题中不正确的一个是
A.若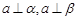 则 则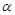 ∥ ∥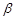 | B.若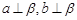 ,则 ,则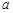 ∥ ∥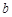 |
C.若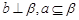 则 则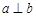 | D.若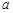 ∥ ∥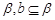 ,则 ,则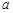 ∥ ∥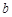 |
设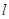 ,
, 是两条不同的直线,
是两条不同的直线, 是一个平面,则下列命题正确的是( )
是一个平面,则下列命题正确的是( )
A.若 , , ,则 ,则 |
B.若 , , ,则 ,则 |
C.若 , , ,则 ,则 |
D.若 , , ,则 ,则 |
设a,b为两条直线, 为两个平面,则下列结论成立的是( )
为两个平面,则下列结论成立的是( )
A.若 且 且 ,则 ,则 | B.若 且 且 ,则 ,则 |
C.若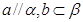 则 则 | D.若 , , ,则 ,则 |
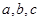 是三条不同的直线,
是三条不同的直线,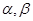 是两个不同的平面,在下列命题:
是两个不同的平面,在下列命题: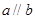 ,且
,且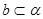 ,则
,则
 ,且
,且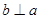 ,则
,则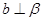
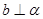 ,则
,则


