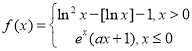Question

【题目】已知椭圆的一个顶点是，离心率为．

（Ⅰ）求椭圆的方程；

（Ⅱ）已知矩形的四条边都与椭圆相切，设直线AB方程为，求矩形面积的最小值与最大值.

Answer 1

【答案】（Ⅰ）；（Ⅱ）当时S有最大值10；当k=0时，S有最小值8.

【解析】

试题（Ⅰ）利用待定系数法即可，由题意，椭圆的一个顶点是，

所以，又，椭圆C的方程是；（Ⅱ）注意斜率的讨论，当时，

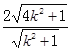椭圆的外切矩形面积为8. 当时， AB所在直线方程为，所以，直线BC和AD的斜率均为.联立直线AB与椭圆方程可得，令得到，直线AB与直线DC之间的距离为，同理可求BC与AD距离为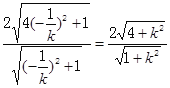，所以矩形ABCD的面积为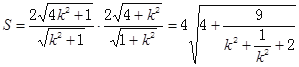，再利用基本不等式即可解决.

试题解析：（Ⅰ）由题意，椭圆的一个顶点是，

所以

又，离心率为，即，

解得，

故椭圆C的方程是

（Ⅱ）当时，

椭圆的外切矩形面积为8.

当时，

椭圆的外切矩形的边AB所在直线方程为，

所以，直线BC和AD的斜率均为.

由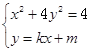，消去y得

，

化简得：

所以，直线AB方程为

直线DC方程为

直线AB与直线DC之间的距离为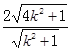

同理，可求BC与AD距离为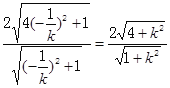

则矩形ABCD的面积为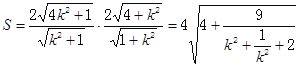

由均值定理

仅当，即时S有最大值10.

因此，当时S有最大值10；

当K=0时，S有最小值8.