题目内容
(本小题满分14分)
已知函数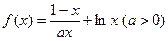 .
.
(1)若函数f(x)在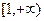 上为增函数,求实数a的取值范围;
上为增函数,求实数a的取值范围;
(2)当a=1时,求f(x)在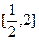 上的最大值和最小值;(注
上的最大值和最小值;(注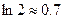 )
)
(3)当a=1时,求证:对大于1的任意正整数n,均有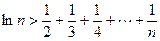 .
.
已知函数
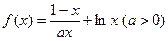 .
.(1)若函数f(x)在
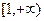 上为增函数,求实数a的取值范围;
上为增函数,求实数a的取值范围;(2)当a=1时,求f(x)在
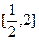 上的最大值和最小值;(注
上的最大值和最小值;(注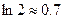 )
)(3)当a=1时,求证:对大于1的任意正整数n,均有
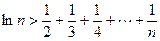 .
.解:(1)由已知得
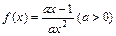
依题意得:
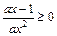 在
在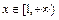 恒成立,
恒成立,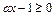 在
在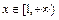 恒成立,即
恒成立,即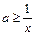 在
在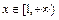 恒成立,
恒成立,所以
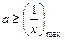 ,得
,得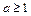
经检验,当时
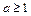 ,函数f(x)在
,函数f(x)在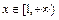 上为增函数
上为增函数(2)当a=1时
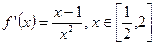
若
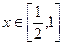 ,则
,则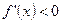 ,若
,若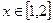 ,则
,则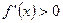 ,故x=1是函数f(x)在区间
,故x=1是函数f(x)在区间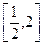 上的惟一的极小值点,也就是最小值点,
上的惟一的极小值点,也就是最小值点,所以当
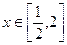 时,f(x)min=f(1)=0.
时,f(x)min=f(1)=0.又
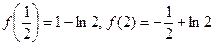 ,
,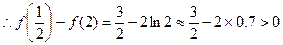
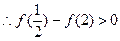 ,即,
,即,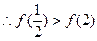
即函数f(x)在区间
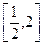 上最大值是
上最大值是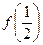 ;
;综上所述,函数f(x)在区间
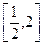 的最大值是1-ln2,最小值是0
的最大值是1-ln2,最小值是0(3)当a=1时,由(1)知,函数
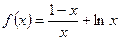 在
在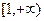 上为增函数,
上为增函数,当n>1时,令
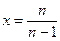 ,则x>1,故f(x)>f(1)=0
,则x>1,故f(x)>f(1)=0即
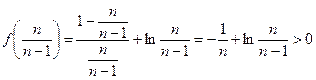 ,即
,即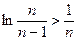
故
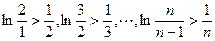
相加得
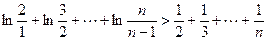
而
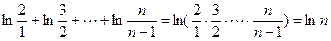
即对于大于1的任意正整数n,
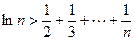
略

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目
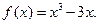
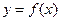 在点
在点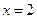 处的切线方程;
处的切线方程;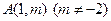 可作曲线
可作曲线 的取值范围.
的取值范围.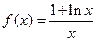

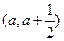 上存在极值,其中a >0,求实数a的取值范围;
上存在极值,其中a >0,求实数a的取值范围;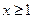 时,不等式
时,不等式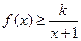 恒成立,求实数k的取值范围;
恒成立,求实数k的取值范围;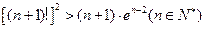 。
。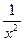 , x
, x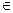
 。
。 ,
, 若
若 ,则
,则 ( )
( ) 移
移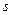 (米)和与时间
(米)和与时间 (秒)的关系为
(秒)的关系为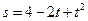 ,则该物体在4秒末的瞬时速度是 ( )
,则该物体在4秒末的瞬时速度是 ( ) ,则
,则 等于( )
等于( ) B
B  C
C  D
D 
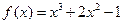 ,则
,则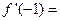 ( )。
( )。 


