题目内容
已知函数f(x)=2ax-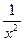 , x
, x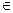
 。
。
(1)若f(x)在x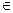
 上是增函数,求a的取值范围;(2)求f(x) 在x
上是增函数,求a的取值范围;(2)求f(x) 在x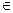
 上的最大值。
上的最大值。
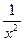 , x
, x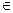
 。
。(1)若f(x)在x
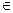
 上是增函数,求a的取值范围;(2)求f(x) 在x
上是增函数,求a的取值范围;(2)求f(x) 在x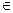
 上的最大值。
上的最大值。(1)由已知可得f′(x)=2a+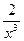 。因为f(x)在x
。因为f(x)在x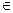
 上是增函数,有
上是增函数,有
f′(x)>0,即有a>-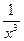 ,而g(x)= -
,而g(x)= -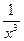 在
在 为增函数,且g(x)的最大值为g(1)= -1,所以a>-1。当a=-1时, f′(x)=2a+
为增函数,且g(x)的最大值为g(1)= -1,所以a>-1。当a=-1时, f′(x)=2a+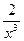 ,在x
,在x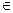
 也有 f′(x)>0,满足f(x)在
也有 f′(x)>0,满足f(x)在 为增函数,所以a≥-1。
为增函数,所以a≥-1。
(2)由(1)知a≥-1时,f(x)在 为增函数,所以当a≥-1时,f(x)的最大值为f(1)=2a-1。当a<-1时,令f′(x)=2a+
为增函数,所以当a≥-1时,f(x)的最大值为f(1)=2a-1。当a<-1时,令f′(x)=2a+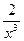 =0,得x=
=0,得x=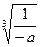 ,注意到0<
,注意到0<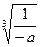 <1,所以当0<x<
<1,所以当0<x<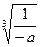 时,
时,
f′(x)>0;当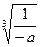 <x≤1时, f′(x)<0,即当a<-1时, f(x)的最大值为f(
<x≤1时, f′(x)<0,即当a<-1时, f(x)的最大值为f(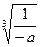 )=-3
)=-3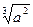 。故对x
。故对x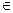
 ,当a≥-1时,f(x)的最大值为2a-1;当a<-1时, f(x)的最大值为-3
,当a≥-1时,f(x)的最大值为2a-1;当a<-1时, f(x)的最大值为-3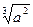 。
。
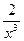 。因为f(x)在x
。因为f(x)在x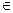
 上是增函数,有
上是增函数,有 f′(x)>0,即有a>-
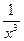 ,而g(x)= -
,而g(x)= -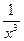 在
在 为增函数,且g(x)的最大值为g(1)= -1,所以a>-1。当a=-1时, f′(x)=2a+
为增函数,且g(x)的最大值为g(1)= -1,所以a>-1。当a=-1时, f′(x)=2a+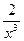 ,在x
,在x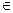
 也有 f′(x)>0,满足f(x)在
也有 f′(x)>0,满足f(x)在 为增函数,所以a≥-1。
为增函数,所以a≥-1。(2)由(1)知a≥-1时,f(x)在
 为增函数,所以当a≥-1时,f(x)的最大值为f(1)=2a-1。当a<-1时,令f′(x)=2a+
为增函数,所以当a≥-1时,f(x)的最大值为f(1)=2a-1。当a<-1时,令f′(x)=2a+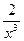 =0,得x=
=0,得x=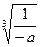 ,注意到0<
,注意到0<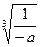 <1,所以当0<x<
<1,所以当0<x<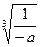 时,
时,f′(x)>0;当
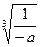 <x≤1时, f′(x)<0,即当a<-1时, f(x)的最大值为f(
<x≤1时, f′(x)<0,即当a<-1时, f(x)的最大值为f(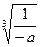 )=-3
)=-3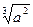 。故对x
。故对x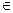
 ,当a≥-1时,f(x)的最大值为2a-1;当a<-1时, f(x)的最大值为-3
,当a≥-1时,f(x)的最大值为2a-1;当a<-1时, f(x)的最大值为-3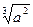 。
。(1)由已知可得f′(x)=2a+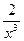 。因为f(x)在x
。因为f(x)在x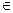
 上是增函数,有
上是增函数,有
f′(x)>0,即有a>-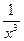 ,而g(x)= -
,而g(x)= -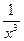 在
在 为增函数,且g(x)的最大值为g(1)= -1,所以a>-1。当a=-1时, f′(x)=2a+
为增函数,且g(x)的最大值为g(1)= -1,所以a>-1。当a=-1时, f′(x)=2a+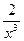 ,在x
,在x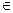
 也有 f′(x)>0,满足f(x)在
也有 f′(x)>0,满足f(x)在 为增函数,所以a≥-1。
为增函数,所以a≥-1。
(2)由(1)知a≥-1时,f(x)在 为增函数,所以当a≥-1时,f(x)的最大值为f(1)=2a-1。当a<-1时,令f′(x)=2a+
为增函数,所以当a≥-1时,f(x)的最大值为f(1)=2a-1。当a<-1时,令f′(x)=2a+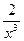 =0,得x=
=0,得x=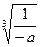 ,注意到0<
,注意到0<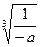 <1,所以当0<x<
<1,所以当0<x<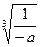 时,
时,
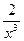 。因为f(x)在x
。因为f(x)在x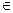
 上是增函数,有
上是增函数,有 f′(x)>0,即有a>-
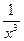 ,而g(x)= -
,而g(x)= -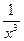 在
在 为增函数,且g(x)的最大值为g(1)= -1,所以a>-1。当a=-1时, f′(x)=2a+
为增函数,且g(x)的最大值为g(1)= -1,所以a>-1。当a=-1时, f′(x)=2a+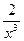 ,在x
,在x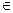
 也有 f′(x)>0,满足f(x)在
也有 f′(x)>0,满足f(x)在 为增函数,所以a≥-1。
为增函数,所以a≥-1。(2)由(1)知a≥-1时,f(x)在
 为增函数,所以当a≥-1时,f(x)的最大值为f(1)=2a-1。当a<-1时,令f′(x)=2a+
为增函数,所以当a≥-1时,f(x)的最大值为f(1)=2a-1。当a<-1时,令f′(x)=2a+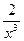 =0,得x=
=0,得x=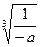 ,注意到0<
,注意到0<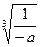 <1,所以当0<x<
<1,所以当0<x<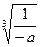 时,
时,
练习册系列答案
相关题目
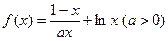 .
.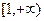 上为增函数,求实数a的取值范围;
上为增函数,求实数a的取值范围;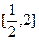 上的最大值和最小值;(注
上的最大值和最小值;(注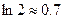 )
)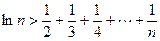 .
.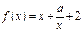 (
(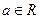 )
)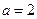 ,求
,求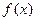 在
在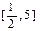 上的最小值和最大值;
上的最小值和最大值;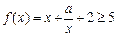 对
对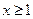 恒成立,求实数
恒成立,求实数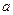 的取值范围
的取值范围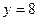 相切,求
相切,求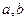 的值;
的值;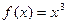 ,导函数值
,导函数值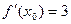 ,则正数
,则正数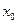 的值
的值 ,且
,且 .
.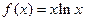 ,若
,若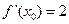 ,则
,则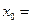 ( )
( )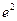




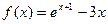 ,则
,则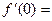 ( )
( )

