题目内容
(本题满分14分)已知函数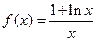

(1)若函数在区间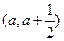 上存在极值,其中a >0,求实数a的取值范围;
上存在极值,其中a >0,求实数a的取值范围;
(2)如果当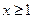 时,不等式
时,不等式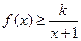 恒成立,求实数k的取值范围;
恒成立,求实数k的取值范围;
(3)求证: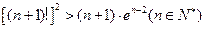 。
。
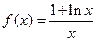

(1)若函数在区间
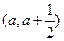 上存在极值,其中a >0,求实数a的取值范围;
上存在极值,其中a >0,求实数a的取值范围;(2)如果当
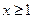 时,不等式
时,不等式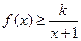 恒成立,求实数k的取值范围;
恒成立,求实数k的取值范围;(3)求证:
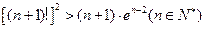 。
。
|

(2)
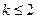
(3)略

(2)不等式
 即为
即为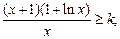 记
记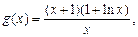
所以
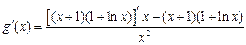
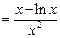 ………… 6分
………… 6分令
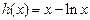 ,则
,则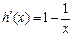 ,
, 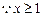 ,
,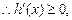
 在
在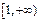 上单调递增,
上单调递增, 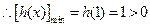 ,从而
,从而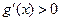 , 故
, 故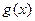 在
在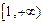 上也单调递增,………… 8分
上也单调递增,………… 8分 所以
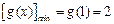 ,所以
,所以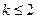 .
. 
 ………… 9分
………… 9分(3)由(2)知:
 恒成立,即
恒成立,即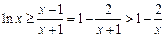 ,
, 令
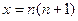 ,则
,则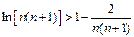 , ………… 11分
, ………… 11分所以
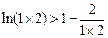 ,
, 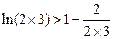 ,
,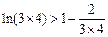 ,
,… …

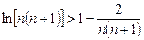 ,
, 叠加得:
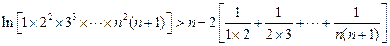
 =n-2(1-
=n-2(1-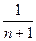 )>n-2+
)>n-2+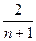 >n-2 . ………… 13分
>n-2 . ………… 13分则
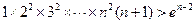 ,所以[(n+1)!]2>(n+1).en-2(n∈N*)………… 14分
,所以[(n+1)!]2>(n+1).en-2(n∈N*)………… 14分
练习册系列答案
 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案
相关题目
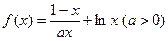 .
.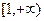 上为增函数,求实数a的取值范围;
上为增函数,求实数a的取值范围;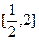 上的最大值和最小值;(注
上的最大值和最小值;(注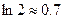 )
)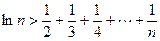 .
.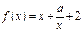 (
(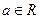 )
)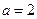 ,求
,求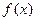 在
在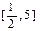 上的最小值和最大值;
上的最小值和最大值;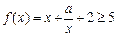 对
对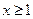 恒成立,求实数
恒成立,求实数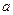 的取值范围
的取值范围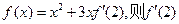 = .
= .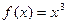 ,导函数值
,导函数值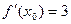 ,则正数
,则正数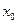 的值
的值 ,且
,且 .
.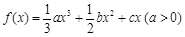 ,记
,记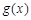 为它的导函数,若
为它的导函数,若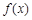 在R上存在反函数,且
在R上存在反函数,且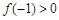 ,则
,则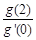 的最小值为( )
的最小值为( )