题目内容
10.函数f(x)=sin(πcos x)在区间[0,2π]上的零点个数是( )| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
分析 由已知可得πcos x∈[-π,π],若sin(πcos x)=0,则πcos x=-π,πcos x=π或πcos x=0,分别求满足条件的x值的个数,最后综合讨论结果,可得答案.
解答 解:当x∈[0,2π]时,
cos x∈[-1,1],
πcos x∈[-π,π],
当πcos x=-π,即cosx=-1,即x=π时,sin(πcos x)=0,
当πcos x=π,即cosx=1,即x=0,或2π时,sin(πcos x)=0,
当πcos x=0,即cosx=0,即,即x=$\frac{1}{2}$π,或x=$\frac{3}{2}$π时,sin(πcos x)=0,
综上所述,函数f(x)=sin(πcos x)在区间[0,2π]上有5零点.
故选:C
点评 本题主要考查了函数零点的意义和判断方法,三角函数的图象和性质,分类讨论思想,难度中档.

练习册系列答案
相关题目
5.在党的群众教育路线总结阶段,一督导组从某单位随机抽调25名员工,对本单位的各项开展工作进行打分评价,现获得如下的数据:70,82,81,76,80,77,77,65,85,69,83,71,76,89,74,73,83,82,72,74,86,79,76,根据上述数据得到样本的频率分布表如下:
(1)确定样本频率分布表中n,m,x,y的值;
(2)根据上述频率分布表,画出样本频率分布直方图;
(3)根据样本频率分布表,求在该单位中任取3名员工的打分,恰有2名员工的打分在(75,85)的概率.
| 分组 | 频数 | 频率 |
| [65,70] | 3 | 0.12 |
| (70,75] | 5 | 0.20 |
| (75,80] | n | x |
| (80,85] | 7 | y |
| (85,90] | m | 0.08 |
(2)根据上述频率分布表,画出样本频率分布直方图;
(3)根据样本频率分布表,求在该单位中任取3名员工的打分,恰有2名员工的打分在(75,85)的概率.
2.已知函数f(x)=$\left\{\begin{array}{l}1-2|x-\frac{1}{2}|,0≤x≤1\\{log_{2014}}x,\;\;\;\;\;x>1\end{array}$,若直线y=m与函数y=f(x)三个不同交点的横坐标依次为x1,x2,x3且x1<x2<x3,则x3的取值范围是( )
| A. | (2,2015) | B. | (1,2015) | C. | (2,2014) | D. | (1,2014) |
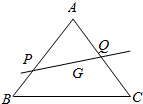 如图,设G为△ABC的重心,过G的直线l分别交AB,AC于P,Q,若$\overrightarrow{AP}$=m$\overrightarrow{AB}$,$\overrightarrow{AQ}$=n$\overrightarrow{AC}$,令$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AC}$=$\overrightarrow{b}$
如图,设G为△ABC的重心,过G的直线l分别交AB,AC于P,Q,若$\overrightarrow{AP}$=m$\overrightarrow{AB}$,$\overrightarrow{AQ}$=n$\overrightarrow{AC}$,令$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AC}$=$\overrightarrow{b}$