题目内容
2.已知函数f(x)=$\left\{\begin{array}{l}1-2|x-\frac{1}{2}|,0≤x≤1\\{log_{2014}}x,\;\;\;\;\;x>1\end{array}$,若直线y=m与函数y=f(x)三个不同交点的横坐标依次为x1,x2,x3且x1<x2<x3,则x3的取值范围是( )| A. | (2,2015) | B. | (1,2015) | C. | (2,2014) | D. | (1,2014) |
分析 作出函数f(x)的图象,利用函数的对称性以及对数函数的图象,即可得到结论.
解答 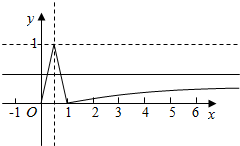 解:作出函数f(x)的图象,
解:作出函数f(x)的图象,
则当0<x<1时,函数f(x)关于x=$\frac{1}{2}$对称,
若直线y=m与函数y=f(x)三个不同交点的横坐标依次为
x1,x2,x3,且x1<x2<x3,
则0<m<1,
且x1,x2关于x=$\frac{1}{2}$对称,则x1+x2=1,
由log2014x=1,得x=2014,
则1<x3<2014,
故选D.
点评 本题主要考查分段函数的应用,考查了函数图象的作法及应用及函数零点与函数图象的有关系,利用数形结合是解决本题的关键.属于中档题.

练习册系列答案
 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
12.从长度分别为2,3,4,5的线段中任取三条,则以这三条线段为边可以构成三角形的概率是( )
| A. | $\frac{3}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
10.函数f(x)=sin(πcos x)在区间[0,2π]上的零点个数是( )
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
17.若$\overrightarrow{AO}+\overrightarrow{OB}+\overrightarrow{CA}+\overrightarrow{OC}+\overrightarrow{BO}$=( )
| A. | $\overrightarrow{AB}$ | B. | $\overrightarrow 0$ | C. | $\overrightarrow{AC}$ | D. | $\overrightarrow{BC}$ |
11.已知集合A={-2,2},B={m|m=x+y,x∈A,y∈A},则集合B等于( )
| A. | {-4,4} | B. | {-4,0,4} | C. | {-4,0} | D. | {0} |