题目内容
8.设函数f(x)=$\left\{\begin{array}{l}3x-1,x<1\\{2^x},x≥1.\end{array}$,则f(1)=2; 若f(a)=1,则a的值为$\frac{2}{3}$.分析 利用分段函数直接求解函数值即可.
解答 解:设函数f(x)=$\left\{\begin{array}{l}3x-1,x<1\\{2^x},x≥1.\end{array}$,则f(1)=2;
f(a)=1,可得3a-1=1,解得a=$\frac{2}{3}$;
2a=1,解得a=0(舍去).
故答案为:2;$\frac{2}{3}$.
点评 本题考查函数值的求法,函数的解析式的应用.

练习册系列答案
相关题目
18.已知F是抛物线y2=x的焦点,A,B是该抛物线上的两点,|AF|+|BF|=3,则线段AB的中点到抛物线准线的距离为( )
| A. | 1 | B. | $\frac{5}{4}$ | C. | $\frac{3}{2}$ | D. | 2 |
3.如图,在复平面内,复数z1和z2对应的点分别是A和B,则$\frac{{z}_{1}}{{z}_{2}}$等于( )
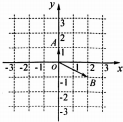

| A. | $\frac{1}{5}$+$\frac{2}{5}$i | B. | $\frac{2}{5}$+$\frac{1}{5}$i | C. | -$\frac{1}{5}$+$\frac{2}{5}$i | D. | -$\frac{2}{5}$+$\frac{1}{5}$i |
18.若loga$\root{7}{b}$=c,则a,b,c之间满足( )
| A. | b7=ac | B. | b=a7c | C. | b=7ac | D. | b=c7a |