题目内容
16．命题p：x2-2x-3＜0，命题q：x2-ax-2a2＜0，若命题p是命题q的必要不充分条件，则实数a的取值范围为$[-\frac{1}{2}，1]$，．分析 先求出关于p，q的x的范围，根据命题p是命题q的必要不充分条件，得到不等式组，解出即可．
解答 解：关于命题p：x2-2x-3＜0，
解不等式得：-1＜x＜3，
关于命题q：x2-ax-2a2＜0，
解不等式得：a＞0时：-a＜x＜2a，a＜0时：2a＜x＜-a，
若命题p是命题q的必要不充分条件，
则$\left\{\begin{array}{l}{a＞0}\\{-a＞-1}\\{2a＜3}\end{array}\right.$或$\left\{\begin{array}{l}{a＜0}\\{2a＞-1}\\{-a＜3}\end{array}\right.$，
解得：0＜a＜1或-$\frac{1}{2}$＜a＜0，a=0时也成立，
则实数a的取值范围为：$[-\frac{1}{2}，1]$，
故答案为：：$[-\frac{1}{2}，1]$．
点评 本题考查了充分必要条件，考查解不等式问题，是一道基础题．
练习册系列答案
相关题目
6．m＜0是方程2x2+7mx+5m2+1=0的两根一根比2大，一根比2小的（ ）
| A． | 必要不充分条件 | B． | 充分不必要条件 | ||
| C． | 充分必要条件 | D． | 既不充分也不必要条件 |
4．定义在R上的偶函数f（x）满足f（2-x）=f（x），且在[-3，-2]上是减函数，a，b是钝角三角形的两个锐角，则下列结论正确的是（ ）
| A． | f（sina）＞f（cosb） | B． | f（sina）＜f（cosb） | C． | f（cosa）＜f（cosb） | D． | f（cosa）＞f（cosb） |
11．已知集合A={x∈R|x2+x-6＞0}，B={x∈R|-π＜x＜e}，则（ ）
| A． | A∩B=∅ | B． | A∪B=R | C． | B⊆∁RA | D． | A⊆B |
1．在边长为1的等边△ABC中，设$\overrightarrow{BC}$=$\overrightarrow{a}$，$\overrightarrow{CA}$=$\overrightarrow{b}$，$\overrightarrow{AB}$=$\overrightarrow{c}$，则$\overrightarrow{a}$•$\overrightarrow{b}$-$\overrightarrow{b}$•$\overrightarrow{c}$+$\overrightarrow{c}$•$\overrightarrow{a}$=（ ）
| A． | $\frac{1}{2}$ | B． | -$\frac{1}{2}$ | C． | $\frac{3}{2}$ | D． | -$\frac{3}{2}$ |
5．
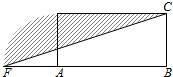设计一个商标图案如图中阴影部分，矩形ABCD中，AB=2BC，且AB=8cm，以点A为圆心，AD为半径作圆与BA的延长线相交于点F，则商标图案的面积等于（ ）
设计一个商标图案如图中阴影部分，矩形ABCD中，AB=2BC，且AB=8cm，以点A为圆心，AD为半径作圆与BA的延长线相交于点F，则商标图案的面积等于（ ）| A． | （4π+8）cm2 | B． | （4π+16）cm2 | C． | （3π+8）cm2 | D． | （3π+16）cm2 |
6．若a=log5$\frac{2}{3}$，b=log8$\sqrt{3}$，c=$\frac{1}{2}$log2$\sqrt{2}$，则a，b，c的大小关系是（ ）
| A． | a＜c＜b | B． | a＜b＜c | C． | c＜a＜b | D． | c＜b＜a |