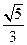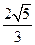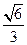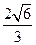题目内容
圆锥的底面半径为5 cm,高为12 cm,当它的内接圆柱的底面半径为何值时,圆锥的内接圆柱全面积有最大值?最大值是多少?
2π(12x-
 )
)  cm2
cm2如图SAB是圆锥的轴截面,其中SO=12,OB=5.设圆锥内接圆柱底面半径为O1C=x,由△SO1C∽△SOB,
则 =
= ,SO1=
,SO1= ·O1C=
·O1C= ,
,
∴OO1=SO-SO1=12- ,
,
则圆柱的全面积S=S侧+2S底=2π(12- )x+2πx2=2π(12x-
)x+2πx2=2π(12x- ).
).
当x= cm时,S取到最大值
cm时,S取到最大值 cm2.
cm2.

则
 =
= ,SO1=
,SO1= ·O1C=
·O1C= ,
,∴OO1=SO-SO1=12-
 ,
,则圆柱的全面积S=S侧+2S底=2π(12-
 )x+2πx2=2π(12x-
)x+2πx2=2π(12x- ).
).当x=
 cm时,S取到最大值
cm时,S取到最大值 cm2.
cm2.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
 (2)若矩形ABCD的一个边AB="3," 另一边BC=2
(2)若矩形ABCD的一个边AB="3," 另一边BC=2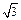 ,EF=2
,EF=2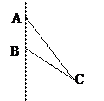
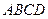 扩建成一个更大的矩形花坛
扩建成一个更大的矩形花坛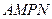 ,要求
,要求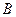 点在
点在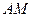 上,
上,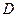 点在
点在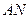 上,且对角线
上,且对角线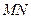 过
过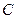 点,已知
点,已知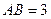 米,
米,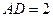 米.
米.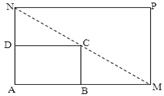
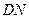 的长应在什么范围内?
的长应在什么范围内?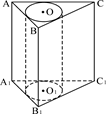

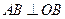 ,垂足为B,
,垂足为B,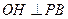 ,垂足为H,且PA=4,C为PA的中点,则当三棱锥O-HPC的体积最大时,OB的长是( )
,垂足为H,且PA=4,C为PA的中点,则当三棱锥O-HPC的体积最大时,OB的长是( )