题目内容
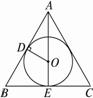
如图，在△ABC中，AB＝3，BC＝5，∠ ABC＝120°，将△ABC绕直线AB旋转一周，则所形成的旋转体的表面积是
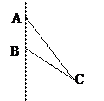
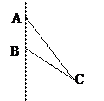
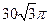
在△ABC中，由余弦定理，得AC＝7.
过点C作CO⊥AB，垂足为O，则OC＝BCsin60°＝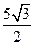
.
由图知，所形成的旋转体的表面积S为圆锥AO和圆锥BO的表面积之和.
所以S＝π×OC×(BC＋AC)＝.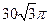
过点C作CO⊥AB，垂足为O，则OC＝BCsin60°＝
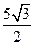.由图知，所形成的旋转体的表面积S为圆锥AO和圆锥BO的表面积之和.
所以S＝π×OC×(BC＋AC)＝
.
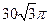练习册系列答案
名校课堂系列答案
相关题目
cm的实心铁球，四个球两两相切，其中底层两球与容器底面相切. 现往容器里注水，使水面恰好浸没所有铁球，则需要注水 cm3.
上一点，求 
．
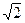的四面体的四个顶点在同一球面上，则此球的表面积为（ ）
？
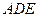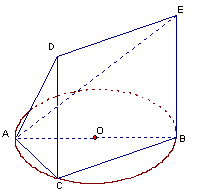
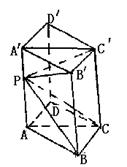
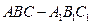的上、下两底边长之比为
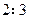，连接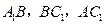
，把正三棱台分成三个三棱锥，求这三个三棱锥的体积之比．
