题目内容
已知直线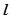 交椭圆
交椭圆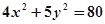 于
于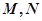 两点,椭圆与
两点,椭圆与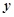 轴的正半轴交于
轴的正半轴交于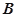 点,若
点,若 的重心恰好落在椭圆的右焦点上,则直线
的重心恰好落在椭圆的右焦点上,则直线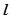 的方程是( )
的方程是( )
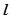 交椭圆
交椭圆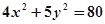 于
于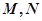 两点,椭圆与
两点,椭圆与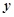 轴的正半轴交于
轴的正半轴交于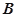 点,若
点,若 的重心恰好落在椭圆的右焦点上,则直线
的重心恰好落在椭圆的右焦点上,则直线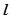 的方程是( )
的方程是( )A.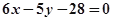 | B.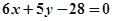 |
C.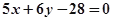 | D.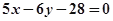 |
A
试题分析:设直线为
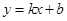 ,与椭圆联立得
,与椭圆联立得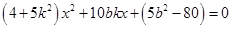
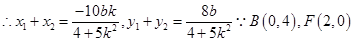

代入得
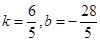 ,直线为
,直线为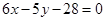
点评:当直线与椭圆相交时,常联立方程组,借助于韦达定理设而不求的方法求解

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目
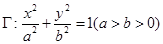 的离心率为
的离心率为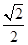 ,且椭圆
,且椭圆 的右焦点
的右焦点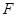 与抛物线
与抛物线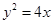 的焦点重合.
的焦点重合.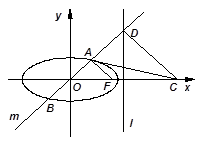
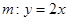 与椭圆
与椭圆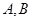 两点(其中点
两点(其中点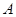 在第一象限),且直线
在第一象限),且直线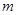 与定直线
与定直线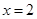 交于点
交于点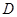 ,过
,过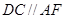 交
交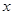 轴于点
轴于点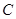 ,试判断直线
,试判断直线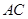 与椭圆
与椭圆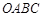 中,
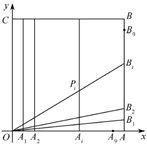
中,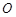 为坐标原点,点
为坐标原点,点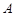 的坐标为
的坐标为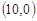 ,点
,点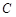 的坐标为
的坐标为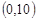 ,分别将线段
,分别将线段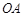 和
和 十等分,分点分别记为
十等分,分点分别记为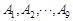 和
和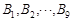 ,连接
,连接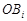 ,过
,过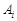 作
作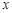 轴的垂线与
轴的垂线与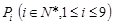 。
。
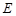 的方程;
的方程;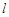 与抛物线E交于不同的两点
与抛物线E交于不同的两点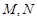 , 若
, 若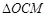 与
与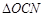 的面积之比为4:1,求直线
的面积之比为4:1,求直线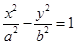 的一个焦点与抛物线
的一个焦点与抛物线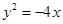 的焦点重合,且双曲线的离心率为
的焦点重合,且双曲线的离心率为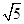 ,则此双曲线的方程为
,则此双曲线的方程为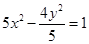
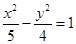
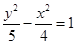
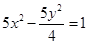
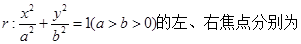
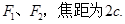 若直线
若直线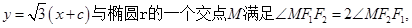 则该椭圆的离心率等于 .
则该椭圆的离心率等于 .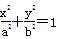 (a>b>0)的左,右焦点,点P是椭圆在y轴右侧上的点,且∠F1PF2=
(a>b>0)的左,右焦点,点P是椭圆在y轴右侧上的点,且∠F1PF2=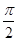 ,记线段PF1与y轴的交点为Q,O为坐标原点,若△F1OQ与四边形OF2PQ的面积之比为1∶2,则该椭圆的离心率等于
,记线段PF1与y轴的交点为Q,O为坐标原点,若△F1OQ与四边形OF2PQ的面积之比为1∶2,则该椭圆的离心率等于 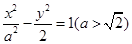 的两条渐近线的夹角为
的两条渐近线的夹角为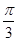 ,则双曲线的离心率为( )
,则双曲线的离心率为( )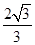
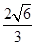
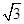
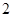
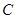 :
: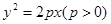 上横坐标为4的点到焦点的距离为5.
上横坐标为4的点到焦点的距离为5.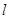 与抛物线
与抛物线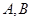 ,若满足
,若满足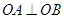 ,证明直线
,证明直线 的坐标.
的坐标.