题目内容
已知双曲线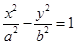
的一个焦点与抛物线
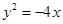的焦点重合,且双曲线的离心率为
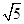,则此双曲线的方程为
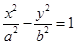的一个焦点与抛物线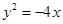的焦点重合,且双曲线的离心率为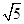,则此双曲线的方程为A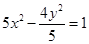． | B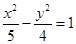． | C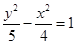． | D． |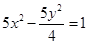
D
试题分析：根据题意，由于双曲线
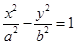的一个焦点与抛物线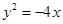的焦点重合，而抛物线的焦点为（-1,0），c="1," 且双曲线的离心率为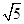,故可知
，因此可知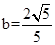
，故可知双曲线方程为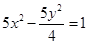，选D.点评：主要是考查了圆锥曲线的性质的运用，属于基础题。
练习册系列答案
黄冈冠军课课练系列答案
相关题目
.
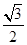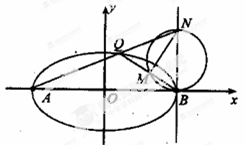
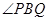的角平分线, 证明直线l过定点. 
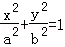（a＞b＞0）的两个焦点分别为F1（﹣1，0），F2（1，0），且椭圆C经过点
．
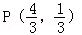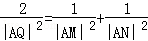，求点Q的轨迹方程．
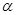平行，P是直线
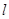上的一定点，平面
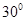。那么B点轨迹是 ( ) 
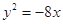的准线过双曲线
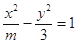的右焦点，则双曲线的离心率为 .
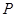到图形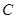
上每一个点的距离的最小值称为点
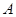的距离相等的点的轨迹不可能是（ ）
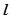交椭圆
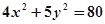于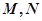
两点，椭圆与
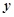轴的正半轴交于
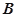点，若
的重心恰好落在椭圆的右焦点上，则直线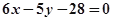
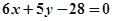
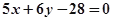
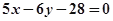
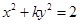表示焦点在y轴上的椭圆，则实数k的取值范围是（ ）