题目内容
9．已知m+n=2e（m，n∈R），那么lnm•lnn的最大值是1．分析 先根据基本不等式得到mn≤$\frac{1}{4}$（m+n）2=e2，再根据基本不等式和对数的运算性质即可得到答案．
解答 解：∵m+n=2e，
∴mn≤$\frac{1}{4}$（m+n）2=e2，
∴lnm•lnn≤$\frac{1}{4}$（lnm+lnn）2=$\frac{1}{4}$ln2（mn）=1，当且仅当m=n=e时取等号，
∴lnm•lnn的最大值是1，
故答案为：1
点评 本题考查了基本不等式的应用，属于基础题
练习册系列答案
举一反三期末百分冲刺卷系列答案
相关题目
15．已知数列{an}满足a1=1，an=logn（n+1）（n≥2，n∈N*）．定义：使乘积a1•a2•a3…an为正整数的k（k∈N+）叫做“幸运数”，则在[1，2015]内所有“幸运数”的和为（ ）
| A． | 2035 | B． | 2036 | C． | 4084 | D． | 4085 |
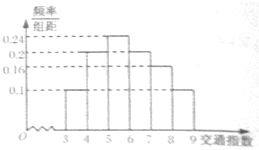交通指数是交通拥堵指数的简称，是综合反映道路间畅通或拥堵的概念．记交通指数为T．其范围为[0，10]，分别有五个级别：T∈[0，2）畅通；T∈[2，4）基本畅通； T∈[4，6）轻度拥堵； T∈[6，8）中度拥堵；T∈[8，10]严重拥堵．早高峰时段（T≥3），从郑州市交通指挥中心随机选取了三环以内的50个交通路段，依据其交通指数数据绘制的频率分布直方图如图 所示：