题目内容
18.高考临近,学校为丰富学生生活,缓解高考压力,特举办一场高三学生队与学校校队的男子篮球比赛.由于爱好者众多,高三学生队队员指定由5班的6人、16班的8人、33班的10人按分层抽样构成一个12人的篮球队.首发阵容有5人组成,要求每个班至少1人,至多2人,则首发方案数为( )| A. | 720 | B. | 270 | C. | 390 | D. | 300 |
分析 求出各个班的人数,然后按照题意求出首发的方案即可.
解答 解:高三学生队队员指定由5班的6人、16班的8人、33班的10人按分层抽样构成一个12人的篮球队.
各个班的人数有5班的3人、16班的4人、33班的5人,
首发共有1、2、2;2、1、2;2、2、1类型;
所求方案有:${C}_{3}^{1}{C}_{4}^{2}{C}_{5}^{2}$+${C}_{3}^{2}{C}_{4}^{1}{C}_{5}^{2}$+${C}_{3}^{2}{C}_{4}^{2}{C}_{5}^{1}$=390.
故选:C.
点评 本题考查排列组合的实际应用,考查分析问题解决问题的能力.

练习册系列答案
相关题目
10.设椭圆C的两个焦点为F1、F2,过点F1的直线与椭圆C交于点M,N,若|MF2|=|F1F2|,且|MF1|=4,|NF1|=3,则椭圆Г的离心率为( )
| A. | $\frac{2}{5}$ | B. | $\frac{3}{5}$ | C. | $\frac{3}{7}$ | D. | $\frac{5}{7}$ |
7.若直线l:ax-by=1与不等式组$\left\{\begin{array}{l}y<1\\ 3x-y-2<0\\ 3x+y+2>0\end{array}\right.$表示的平面区域无公共点,则3a-2b的最小值为( )
| A. | $\frac{7}{2}$ | B. | $-\frac{11}{2}$ | C. | 2 | D. | -2 |
8.已知集合A={-1,i},i为虚数单位,则下列选项正确的是( )
| A. | $\frac{1}{i}$∈A | B. | $\frac{1-i}{1+i}$∈A | C. | i3∈A | D. | |-i|∈A |
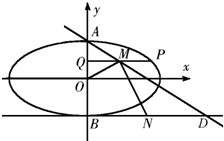 如图,已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的离心率是$\frac{{\sqrt{3}}}{2}$,A,B分别是C的上下顶点,点B在直线l:y=-1上.
如图,已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的离心率是$\frac{{\sqrt{3}}}{2}$,A,B分别是C的上下顶点,点B在直线l:y=-1上.