题目内容
4.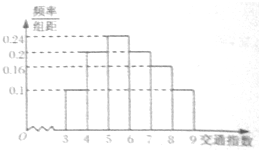 交通指数是交通拥堵指数的简称,是综合反映道路间畅通或拥堵的概念.记交通指数为T.其范围为[0,10],分别有五个级别:T∈[0,2)畅通;T∈[2,4)基本畅通; T∈[4,6)轻度拥堵; T∈[6,8)中度拥堵;T∈[8,10]严重拥堵.早高峰时段(T≥3),从郑州市交通指挥中心随机选取了三环以内的50个交通路段,依据其交通指数数据绘制的频率分布直方图如图 所示:
交通指数是交通拥堵指数的简称,是综合反映道路间畅通或拥堵的概念.记交通指数为T.其范围为[0,10],分别有五个级别:T∈[0,2)畅通;T∈[2,4)基本畅通; T∈[4,6)轻度拥堵; T∈[6,8)中度拥堵;T∈[8,10]严重拥堵.早高峰时段(T≥3),从郑州市交通指挥中心随机选取了三环以内的50个交通路段,依据其交通指数数据绘制的频率分布直方图如图 所示:(Ⅰ)据此频率分布直方图估算交通指数T∈[3,9]时的中位数和平均数;
(Ⅱ)据此频率分布直方图求出该市早高峰三环以内的3个路段至少有两个严重拥堵的概率是多少?
(Ⅲ)某人上班路上所用时间若畅通时为25分钟,基本畅通为35分钟,轻度拥堵为40分钟;中度拥堵为50分钟;严重拥堵为60分钟,求此人所用时间的数学期望.
分析 (Ⅰ)直接利用频率分布表求出T∈[3,9]时交通指数的中位数,T∈[3,9]时交通指数的平均数即可.
(Ⅱ)设事件A为“一条路段严重拥堵”,则P(A)=0.1,利用独立重复试验的概率求解3条路段中DP至少有两条路段严重拥堵的概率.
(Ⅲ)列出所用时间x的分布列,然后求解期望即可.
解答 解:(Ⅰ)由直方图知:T∈[3,9]时交通指数的中位数为5+1×$\frac{0.2}{0.24}$=$\frac{35}{6}$…(2分)T∈[3,9]时交通指数的平均数3.5×0.1+4.5×0.2+5.5×0.24+6.5×0.2+7.5×0.16+8.5×0.1=5.92…(4分)
(Ⅱ)设事件A为“一条路段严重拥堵”,则P(A)=0.1…(5分)
则3条路段中DP至少有两条路段严重拥堵的概率为:$P=C_3^2×{({\frac{1}{10}})^2}×({1-\frac{1}{10}})+C_3^3×{({\frac{1}{10}})^3}=\frac{7}{250}$…(7分)
∴3条路段中至少有两条路段严重拥堵的MQ概率为$\frac{7}{250}$…(8分)
(Ⅲ)由题意,所用时间x的分布列如下表:
| x | 35 | 40 | 50 | 60 |
| P | 0.1 | 0.44 | 0.36 | 0.1 |
∴此人经过该路段所用时间的数学期望是45.1分钟…(12分)
点评 本题考查离散型独立重复试验的概率的求法,频率分布直方图的应用,期望的求法,考查计算能力.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
12.在等差数列{an}中,已知a2=3,公差d=2,设bn=$\frac{2}{{a}_{n}{a}_{n+1}}$,则数列{bn}的前n项和Tn=( )
| A. | $\frac{1}{2n+1}$ | B. | $\frac{2n+2}{2n+1}$ | C. | $\frac{2n}{2n+1}$ | D. | $\frac{n}{2n+1}$ |
19.已知集合U={1,2,3,4,5},A={1,4},B={2,3},则A∩(∁uB)等于( )
| A. | {1,4,5} | B. | {1,4} | C. | {4} | D. | {1,2,3,4} |
14.已知B(-2,0),C(2,0),A为动点,△ABC的周长为10,则动点A的满足的方程为( )
| A. | $\frac{x^2}{6}+\frac{y^2}{5}$=1 | B. | $\frac{x^2}{9}+\frac{y^2}{5}$=1 | C. | $\frac{x^2}{9}+\frac{y^2}{4}$=1 | D. | $\frac{x^2}{8}+\frac{y^2}{4}$=1 |