题目内容
20.若2×4a-2a×3b+2×9b=2a+3b+1,求2a+3b的最大值.分析 先设设2a=m,3b=n,再利用基本不等式得到$\frac{3}{4}$(m+n)2-(m+n)-1≤0,再设m+n=t,t>0,得到关于t的不等式,解得即可得到2a+3b的最大值
解答 解:设2a=m,3b=n,
∵2×4a-2a×3b+2×9b=2a+3b+1,
∴2m2-mn+2n2=m+n+1,
∴2m2+4mn+2n2=m+n+1+5mn,
∴2(m+n)2≤m+n+$\frac{5}{4}$(m+n)2+1,当且仅当m=n时取等号,即a=b=0时取等号,
再设m+n=t,t>0,
∴$\frac{3}{4}$t2-t-1≤0,
解得0<t≤2,
故t的最大值为2,
即2a+3b的最大值为2.
点评 本题考查了基本不等式的应用以及不等式的解法,关键是换元,属于中档题.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
6.在边长为1的正三角形ABC中,|$\overrightarrow{AB}$-$\overrightarrow{BC}$|的值为( )
| A. | 1 | B. | 2 | C. | $\frac{\sqrt{3}}{2}$ | D. | $\sqrt{3}$ |
12.在等差数列{an}中,已知a2=3,公差d=2,设bn=$\frac{2}{{a}_{n}{a}_{n+1}}$,则数列{bn}的前n项和Tn=( )
| A. | $\frac{1}{2n+1}$ | B. | $\frac{2n+2}{2n+1}$ | C. | $\frac{2n}{2n+1}$ | D. | $\frac{n}{2n+1}$ |
10.设椭圆C的两个焦点为F1、F2,过点F1的直线与椭圆C交于点M,N,若|MF2|=|F1F2|,且|MF1|=4,|NF1|=3,则椭圆Г的离心率为( )
| A. | $\frac{2}{5}$ | B. | $\frac{3}{5}$ | C. | $\frac{3}{7}$ | D. | $\frac{5}{7}$ |
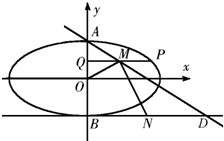 如图,已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的离心率是$\frac{{\sqrt{3}}}{2}$,A,B分别是C的上下顶点,点B在直线l:y=-1上.
如图,已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的离心率是$\frac{{\sqrt{3}}}{2}$,A,B分别是C的上下顶点,点B在直线l:y=-1上.