题目内容
 如图,在梯形ABCD中,AB∥CD,AB=a,CD=b(a>b).若EF∥AB,EF到CD与AB的距离之比为m:n,则可推算出:EF=
如图,在梯形ABCD中,AB∥CD,AB=a,CD=b(a>b).若EF∥AB,EF到CD与AB的距离之比为m:n,则可推算出:EF=| ma+nb |
| m+n |
分析:在平面几何中的进行几何性质类比推理时,我们常用的思路是:由平面几何中线段的性质,类比推理平面几何中面积的性质;故由:EF=
,类比到S0与S1,S2的关系是:
=
.
| ma+nb |
| m+n |
| S0 |
m
| ||||
| m+n |
解答:解:在平面几何中类比几何性质时,
一般为:由平面几何点的性质,类比推理线的性质;
由平面几何中线段的性质,类比推理空间几何中面积的性质;
故由:“EF=
”,
类比到关于△OEF的面积S0与S1,S2的结论是:
=
.
故选C.
一般为:由平面几何点的性质,类比推理线的性质;
由平面几何中线段的性质,类比推理空间几何中面积的性质;
故由:“EF=
| ma+nb |
| m+n |
类比到关于△OEF的面积S0与S1,S2的结论是:
| S0 |
m
| ||||
| m+n |
故选C.
点评:本题考查的知识点是类比推理,类比推理的一般步骤是:(1)找出两类事物之间的相似性或一致性;(2)用一类事物的性质去推测另一类事物的性质,得出一个明确的命题(猜想).

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
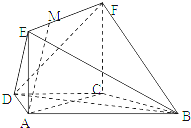 如图,在梯形ABCD中,AB∥CD,AD=DC=CB=a,.∠ABC=60°,平面ACFE⊥平面ABCD,四边形ACFE是矩形,AE=a,点M在线段EF上.
如图,在梯形ABCD中,AB∥CD,AD=DC=CB=a,.∠ABC=60°,平面ACFE⊥平面ABCD,四边形ACFE是矩形,AE=a,点M在线段EF上.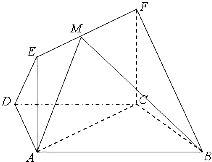 如图,在梯形ABCD中,AB∥CD,AD=DC=CB=1,∠ABC=60°,四边形ACFE为矩形,平面ACFE⊥平面ABCD,CF=1.
如图,在梯形ABCD中,AB∥CD,AD=DC=CB=1,∠ABC=60°,四边形ACFE为矩形,平面ACFE⊥平面ABCD,CF=1.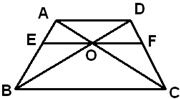 如图,在梯形ABCD中,AD∥BC,BD与AC相交于O,过O的直线分别交AB、CD于E、F,且EF∥BC,若AD=12,BC=20,则EF=
如图,在梯形ABCD中,AD∥BC,BD与AC相交于O,过O的直线分别交AB、CD于E、F,且EF∥BC,若AD=12,BC=20,则EF= 如图,在梯形ABCD中,对角线AC和BD交于点O,E、F分别是AC和BD的中点,分别写出
如图,在梯形ABCD中,对角线AC和BD交于点O,E、F分别是AC和BD的中点,分别写出 如图,在梯形△ABCD中,AB∥CD,AD=DC-=CB=1,么ABC-60.,四边形ACFE为矩形,平面ACFE上平面ABCD,CF=1.
如图,在梯形△ABCD中,AB∥CD,AD=DC-=CB=1,么ABC-60.,四边形ACFE为矩形,平面ACFE上平面ABCD,CF=1.