题目内容
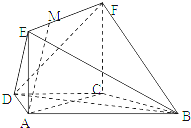 如图,在梯形ABCD中,AB∥CD,AD=DC=CB=a,.∠ABC=60°,平面ACFE⊥平面ABCD,四边形ACFE是矩形,AE=a,点M在线段EF上.
如图,在梯形ABCD中,AB∥CD,AD=DC=CB=a,.∠ABC=60°,平面ACFE⊥平面ABCD,四边形ACFE是矩形,AE=a,点M在线段EF上.(1)求证:BC⊥平面ACFE;
(2)当EM为何值时,AM∥平面BDF?证明你的结论;
(3)求二面角B-EF-D的平面角的余弦值.
分析:(1)由已知中梯形ABCD中,AB∥CD,AD=DC=CB=a,∠ABC=60°,我们易求出AC⊥BC,结合已知中平面ACFE⊥平面ABCD,及平面与平面垂直的性质定理,即可得到BC⊥平面ACFE.
(2)以点ABC-A1B1C1为原点,△ABC所在直线为坐标轴,建立空间直角坐标系,看出AM∥平面BDF等价于
与
、
共面,也等价于存在实数m、n,使
=m
+n
,根据向量之间的关系得到结论.
(3)要求两个平面所成的角,根据向量的加减运算做出平面的法向量,二面角B-EF-D的大小就是向量
与向量
所夹的角.根据向量的夹角做出结果.
(2)以点ABC-A1B1C1为原点,△ABC所在直线为坐标轴,建立空间直角坐标系,看出AM∥平面BDF等价于
| AM |
| FB |
| FD |
| AM |
| FB |
| FD |
(3)要求两个平面所成的角,根据向量的加减运算做出平面的法向量,二面角B-EF-D的大小就是向量
| GD |
| FB |
解答:证明:(1)在梯形ABCD中,∵AB∥CD,
∴四边形ABCD是等腰梯形,
且∠DCA=∠DAC=30°,∠DCB=120°
∴∠ACB=∠DCB-∠DCA=90°
∴AC⊥BC
又∵平面ACFE⊥平面ABCD,交线为AC,
∴BC⊥平面ACFE
解:(2)当EM=
a时,AM∥平面BDF,
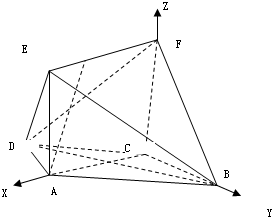
以点ABC-A1B1C1为原点,△ABC所在直线为坐标轴,建立空间直角坐标系,则A(
a,0,0),E(
a,0,a)
AM∥平面BDF?
与
、
共面,也等价于存在实数m、n,使
=m
+n
,
设
=t
.
∵
=(-
a,0,0),
=(-
at,0,0)
∴
=
+
=(-
at,0,0)
又
=(
a,-
a,-a),
=(0,a,-a),
从而要使得:(-
at,0,a)=m(0,a,-a)+n(
a,-
a,-a)成立,
需
,解得t=
∴当EM=
a时,AM∥平面BDF
(3B(0,a,0),A(
a,0,0),
过D作DG⊥EF,垂足为G.令
=λ
=λ(
a,0,0),
=
+
=(
aλ,0,a),
=
-
=(
λa-
a,
a,a)
由
⊥
得,
•
=0,
∴λ=
∴
=(0,
a,a),即
=(0,-
a,-a)
∵BC⊥AC,AC∥EF,
∴BC⊥EF,BF⊥EF
∴二面角B-EF-D的大小就是向量
与向量
所夹的角.
∵
=(0,a,-a)
cos<
,
>=
,即二面角B-EF-D的平面角的余弦值为
.
∴四边形ABCD是等腰梯形,
且∠DCA=∠DAC=30°,∠DCB=120°
∴∠ACB=∠DCB-∠DCA=90°
∴AC⊥BC
又∵平面ACFE⊥平面ABCD,交线为AC,
∴BC⊥平面ACFE
解:(2)当EM=
| ||
| 3 |
以点ABC-A1B1C1为原点,△ABC所在直线为坐标轴,建立空间直角坐标系,则A(
| 3 |
| 3 |
AM∥平面BDF?
| AM |
| FB |
| FD |
| AM |
| FB |
| FD |
设
| EM |
| EF |
∵
| EF |
| 3 |
| EM |
| 3 |
∴
| AM |
| AE |
| EM |
| 3 |
又
| FD |
| ||
| 2 |
| 1 |
| 2 |
| FB |
从而要使得:(-
| 3 |
| ||
| 2 |
| 1 |
| 2 |
需
|
| 1 |
| 3 |
| ||
| 3 |
(3B(0,a,0),A(
| 3 |
过D作DG⊥EF,垂足为G.令
| FG |
| FE |
| 3 |
| CG |
| CF |
| FG |
| 3 |
| DG |
| CG |
| CD |
| 3 |
| ||
| 2 |
| 1 |
| 2 |
由
| DG |
| EF |
| DG |
| EF |
∴λ=
| 1 |
| 2 |
∴
| DG |
| 1 |
| 2 |
| GD |
| 1 |
| 2 |
∵BC⊥AC,AC∥EF,
∴BC⊥EF,BF⊥EF
∴二面角B-EF-D的大小就是向量
| GD |
| FB |
∵
| FB |
cos<
| GD |
| FB |
| ||
| 10 |
| ||
| 10 |

点评:本题考查用空间向量求平面间的夹角和线面之间的关系问题,本题解题的关键是建立适当的坐标系,写出要用的空间向量,把立体几何的理论推导变成数字的运算,这是新课标高考卷中常见的一种题目.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
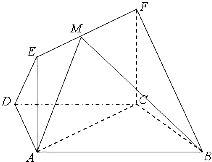 如图,在梯形ABCD中,AB∥CD,AD=DC=CB=1,∠ABC=60°,四边形ACFE为矩形,平面ACFE⊥平面ABCD,CF=1.
如图,在梯形ABCD中,AB∥CD,AD=DC=CB=1,∠ABC=60°,四边形ACFE为矩形,平面ACFE⊥平面ABCD,CF=1.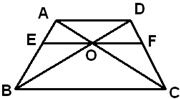 如图,在梯形ABCD中,AD∥BC,BD与AC相交于O,过O的直线分别交AB、CD于E、F,且EF∥BC,若AD=12,BC=20,则EF=
如图,在梯形ABCD中,AD∥BC,BD与AC相交于O,过O的直线分别交AB、CD于E、F,且EF∥BC,若AD=12,BC=20,则EF= 如图,在梯形ABCD中,对角线AC和BD交于点O,E、F分别是AC和BD的中点,分别写出
如图,在梯形ABCD中,对角线AC和BD交于点O,E、F分别是AC和BD的中点,分别写出 如图,在梯形△ABCD中,AB∥CD,AD=DC-=CB=1,么ABC-60.,四边形ACFE为矩形,平面ACFE上平面ABCD,CF=1.
如图,在梯形△ABCD中,AB∥CD,AD=DC-=CB=1,么ABC-60.,四边形ACFE为矩形,平面ACFE上平面ABCD,CF=1.