题目内容
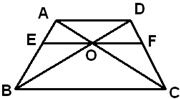如图，在梯形ABCD中，AD∥BC，BD与AC相交于O，过O的直线分别交AB、CD于E、F，且EF∥BC，若AD=12，BC=20，则EF=分析：由已知中EF∥AD∥BC，我们易得到OAD∽△OCB，△OAE∽△CAB，进而我们可以求出AD，EF，BC三条平行线段分线段所成的比例，结合AD=12，BC=20，即可求出答案．
解答：解：∵EF∥AD∥BC，
∴△OAD∽△OCB，
OA：OC=AD：BC=12：20
△OAE∽△CAB
OE：BC=OA：CA=12：32
∴EF=2×
×20=15
故答案为：15
∴△OAD∽△OCB，
OA：OC=AD：BC=12：20
△OAE∽△CAB
OE：BC=OA：CA=12：32
∴EF=2×
| 12 |
| 32 |
故答案为：15
点评：本题考查的知识点是平等线分线段成比例定理，其中求出平行线分线段所成的比例是解答本题的关键．
练习册系列答案
智能训练练测考系列答案
相关题目
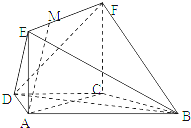如图，在梯形ABCD中，AB∥CD，AD=DC=CB=a，．∠ABC=60°，平面ACFE⊥平面ABCD，四边形ACFE是矩形，AE=a，点M在线段EF上．
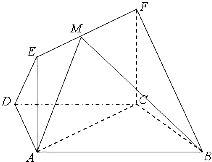如图，在梯形ABCD中，AB∥CD，AD=DC=CB=1，∠ABC=60°，四边形ACFE为矩形，平面ACFE⊥平面ABCD，CF=1．
如图，在梯形ABCD中，对角线AC和BD交于点O，E、F分别是AC和BD的中点，分别写出
如图，在梯形△ABCD中，AB∥CD，AD=DC-=CB=1，么ABC-60．，四边形ACFE为矩形，平面ACFE上平面ABCD，CF=1．