��Ŀ����
��2013•������һģ����ƽ��ֱ������ϵxOy�У���ԲC������Ϊԭ�㣬����F1��F2��x���ϣ�������Ϊ
����F1��ֱ�߽���ԲC��A��B���㣬�ҡ�ABF2���ܳ�Ϊ8��������M��0��3����ֱ��l1����ԲC����G��H���㣨��G�ڵ�M��H֮�䣩��
���� ����ԲC�ķ��̣�
������ֱ��l1��б��k��0����x�����Ƿ���ڵ�P��m��0����ʹ����PG��PHΪ�ڱߵ�ƽ���ı���Ϊ���Σ�������ڣ����m��ȡֵ��Χ����������ڣ���˵�����ɣ�
| 1 | 2 |
���� ����ԲC�ķ��̣�
������ֱ��l1��б��k��0����x�����Ƿ���ڵ�P��m��0����ʹ����PG��PHΪ�ڱߵ�ƽ���ı���Ϊ���Σ�������ڣ����m��ȡֵ��Χ����������ڣ���˵�����ɣ�
��������I��������Բ�������ʼ��㹫ʽe=
���䶨�弴�ɵõ�a��b��c���������ɵõ���Բ�ı����̣�
��II����ֱ��l1�ķ���Ϊy=kx+3��k��0��������Բ�ķ�����������ֱ������Բ��������ͬ�Ľ���?����0���ɵ�k��ȡֵ��Χ���������ϵ���Ĺ�ϵ��
����x�����Ƿ���ڵ�P��m��0����ʹ����PG��PHΪ�ڱߵ�ƽ���ı���Ϊ���Σ����ȼ��ڡ���x�����Ƿ���ڵ�P��m��0����ʹ��PN��l1�������ɵõ���k��ʾm�����õ������ɵó�ȡֵ��Χ��
| c |
| a |
��II����ֱ��l1�ķ���Ϊy=kx+3��k��0��������Բ�ķ�����������ֱ������Բ��������ͬ�Ľ���?����0���ɵ�k��ȡֵ��Χ���������ϵ���Ĺ�ϵ��
����x�����Ƿ���ڵ�P��m��0����ʹ����PG��PHΪ�ڱߵ�ƽ���ı���Ϊ���Σ����ȼ��ڡ���x�����Ƿ���ڵ�P��m��0����ʹ��PN��l1�������ɵõ���k��ʾm�����õ������ɵó�ȡֵ��Χ��
����⣺��������Բ�ķ���Ϊ
+
=1(a��b��0)��������e=
=
��
��ABF2���ܳ�Ϊ|AF1|+|AF2|+|AF1|+|AF2|=4a=8��
���a=2��c=1����b2=a2-c2=3��
������Բ�ķ���Ϊ
+
=1��
����ֱ��l1�ķ���Ϊy=kx+3��k��0����
��
����ȥy�������ã�3+4k2��x2+24kx+24=0��*����
��=��24k��2-4��24����3+4k2����0�����k��
��
����Բ����GH���е�ΪN��x0��y0����
����x�����Ƿ���ڵ�P��m��0����ʹ����PG��PHΪ�ڱߵ�ƽ���ı���Ϊ���Σ����ȼ��ڡ���x�����Ƿ���ڵ�P��m��0����ʹ��PN��l1����
��G��x1��y1����H��x2��y2������Τ�ﶨ���ã�x1+x2=-
��
����x0=
=-
����y0=kx0+3�T
��
��N(-
��
)��kPN=-
��
���ԣ�-
•k=-1�����m=-
(k��
)��
m��(k)=
��
��0��
���ԣ�����m=-
(k��
)�ڶ�����(
��+��)����������m(
)=-
��
�������������ĵ�P��m��0�����ڣ�m��ȡֵ��ΧΪ(-
��+��)��
| x2 |
| a2 |
| y2 |
| b2 |
| c |
| a |
| 1 |
| 2 |
��ABF2���ܳ�Ϊ|AF1|+|AF2|+|AF1|+|AF2|=4a=8��
���a=2��c=1����b2=a2-c2=3��
������Բ�ķ���Ϊ
| x2 |
| 4 |
| y2 |
| 3 |
����ֱ��l1�ķ���Ϊy=kx+3��k��0����
��
|
��=��24k��2-4��24����3+4k2����0�����k��
| ||
| 2 |
����Բ����GH���е�ΪN��x0��y0����
����x�����Ƿ���ڵ�P��m��0����ʹ����PG��PHΪ�ڱߵ�ƽ���ı���Ϊ���Σ����ȼ��ڡ���x�����Ƿ���ڵ�P��m��0����ʹ��PN��l1����
��G��x1��y1����H��x2��y2������Τ�ﶨ���ã�x1+x2=-
| 24k |
| 3+4k2 |
����x0=
| x1+x2 |
| 2 |
| 12k |
| 3+4k2 |
| 9 |
| 3+4k2 |
��N(-
| 12k |
| 3+4k2 |
| 9 |
| 3+4k2 |
| 9 |
| 12k+m(3+4k2) |
���ԣ�-
| 9 |
| 12k+m(3+4k2) |
| 3k |
| 3+4k2 |
| ||
| 2 |
m��(k)=
3(2k-
| ||||
| (3+4k2)2 |
3(
| ||||||
| (3+4k2)2 |
���ԣ�����m=-
| 3k |
| 3+4k2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 6 |
�������������ĵ�P��m��0�����ڣ�m��ȡֵ��ΧΪ(-
| ||
| 6 |
�����������ۺϿ�������Բ�Ķ��塢�����̼������ʡ�ֱ������Բ�ཻ����ת��Ϊ���������õ�����ϵ���Ĺ�ϵ�����õ����о������ĵ����ԵȻ���֪ʶ�����ģʽ����Ҫ��ǿ�����������ͼ���������

��ϰ��ϵ�д�
�����Ŀ
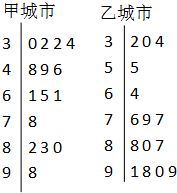 ��2013•������һģ����������ָ��PM2.5����λ����g/m3����ʾÿ���������п���ο�����ĺ��������ֵԽ�ߣ��ʹ���������ȾԽ���أ�
��2013•������һģ����������ָ��PM2.5����λ����g/m3����ʾÿ���������п���ο�����ĺ��������ֵԽ�ߣ��ʹ���������ȾԽ���أ� ��2013•������һģ����ͼ������P-ABCD�ĵ���ABCDΪ���Σ���ABC=60�㣬PA�͵���ABCD��PA=AB=2��EΪPA���е㣮
��2013•������һģ����ͼ������P-ABCD�ĵ���ABCDΪ���Σ���ABC=60�㣬PA�͵���ABCD��PA=AB=2��EΪPA���е㣮