题目内容
（2013•延庆县一模）已知函数f（x）=ax3+bx2-2（a≠0）有且仅有两个不同的零点x1，x2，则（ ）
分析：求导数可得x=0，或x=-
时，函数取得极值，要满足题意需f（-
）=0，可得a，b的关系，当a＞0时，x1+x2的正负不确定，不合题意；当a＜0，可得x1x2＜0，x1+x2＞0，进而可得答案．
| 2b |
| 3a |
| 2b |
| 3a |
解答：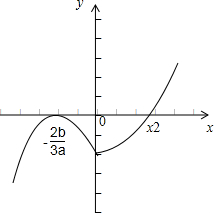
解：原函数的导函数为f′（x）=3ax2+2bx=x（3ax+2b），
令f′（x）=0，可解得x=0，或x=-
，
故当x=0，或x=-
时，函数取得极值，又f（0）=-2＜0，
所以要使函数f（x）=ax3+bx2-2（a≠0）有且仅有两个不同的零点，
则必有f（-
）=a(-
)3+b(-
)2-2=0，解得b3=
，且b＞0，
即函数的一根为x1=-
，
（1）如下图，若a＞0，可知x1=-
＜0，且为函数的极大值点，x=x2处为函数的极小值点，
此时函数有2个零点：-
，x2＞0，显然有x1x2＜0，但x1+x2的正负不确定，故可排除C，D；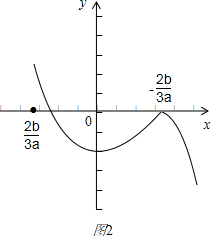
（2）如图2，若a＜0，必有x1=-
＞0，此时必有x1x2＜0，x1=-
的对称点为x=
，
则f（
）=a(
)3+b(
)2-2=
-2=
×
-2=8＞0，
则必有x2＞
，即x2-
＞0，即x1+x2＞0
故选B
解：原函数的导函数为f′（x）=3ax2+2bx=x（3ax+2b），令f′（x）=0，可解得x=0，或x=-
| 2b |
| 3a |
故当x=0，或x=-
| 2b |
| 3a |
所以要使函数f（x）=ax3+bx2-2（a≠0）有且仅有两个不同的零点，
则必有f（-
| 2b |
| 3a |
| 2b |
| 3a |
| 2b |
| 3a |
| 27a2 |
| 2 |
即函数的一根为x1=-
| 2b |
| 3a |
（1）如下图，若a＞0，可知x1=-
| 2b |
| 3a |
此时函数有2个零点：-
| 2b |
| 3a |
（2）如图2，若a＜0，必有x1=-
| 2b |
| 3a |
| 2b |
| 3a |
| 2b |
| 3a |
则f（
| 2b |
| 3a |
| 2b |
| 3a |
| 2b |
| 3a |
| 20b3 |
| 27a2 |
| 20 |
| 27a2 |
| 27a2 |
| 2 |
则必有x2＞
| 2b |
| 3a |
| 2b |
| 3a |
故选B
点评：本题考查根的存在性及根的个数的判断，涉及三次函数的图象以及分类讨论的思想，属中档题
练习册系列答案
相关题目
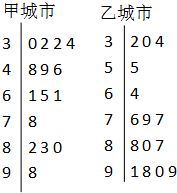（2013•延庆县一模）空气质量指数PM2.5（单位：μg/m3）表示每立方米空气中可入肺颗粒物的含量，这个值越高，就代表空气污染越严重：
（2013•延庆县一模）如图，四棱锥P-ABCD的底面ABCD为菱形，∠ABC=60°，PA⊥底面ABCD，PA=AB=2，E为PA的中点．