题目内容
 (2013•延庆县一模)如图,四棱锥P-ABCD的底面ABCD为菱形,∠ABC=60°,PA⊥底面ABCD,PA=AB=2,E为PA的中点.
(2013•延庆县一模)如图,四棱锥P-ABCD的底面ABCD为菱形,∠ABC=60°,PA⊥底面ABCD,PA=AB=2,E为PA的中点.(Ⅰ)求证:PC∥平面EBD;
(Ⅱ)求三棱锥C-PAD的体积VC-PAD;
(Ⅲ)在侧棱PC上是否存在一点M,满足PC⊥平面MBD,若存在,求PM的长;若不存在,说明理由.
分析:(I)利用菱形的性质可得F为AC的中点,再利用三角形的中位线定理可得EF∥PC,利用线面平行的判定定理即可得出;
(II)由已知PA⊥底面ABCD,可得PA为三棱锥P-ACD的高,利用VC-PAD=VP-ACD及三棱锥的体积计算公式即可得出;
(III)利用三垂线定理可得BD⊥PC,在平面PBC内,作BM⊥PC,垂足为M,求得PM的长即可知道点M是否在线段PC即可.
(II)由已知PA⊥底面ABCD,可得PA为三棱锥P-ACD的高,利用VC-PAD=VP-ACD及三棱锥的体积计算公式即可得出;
(III)利用三垂线定理可得BD⊥PC,在平面PBC内,作BM⊥PC,垂足为M,求得PM的长即可知道点M是否在线段PC即可.
解答:(Ⅰ)证明:设AC、BD相交于点F,连接EF,
∵ABCD底面ABCD为菱形,∴F为AC的中点,
又∵E为PA的中点,∴EF∥PC.
又∵EF?平面EBD,PC?平面EBD,
∴PC∥平面EBD.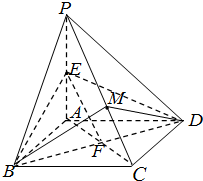
(Ⅱ)解:∵底面ABCD为菱形,∠ABC=60°,
∴△ACD是边长为2正三角形,
又∵PA⊥底面ABCD,∴PA为三棱锥P-ACD的高,
∴VC-PAD=VP-ACD=
S△ACD•PA=
×
×22×2=
.
(Ⅲ)解:在侧棱PC上存在一点M,满足PC⊥平面MBD,下面给出证明.
∵PA⊥底面ABCD,
又ABCD底面ABCD为菱形,∴AC⊥BD,
∵BD?平面ABCD,
∴BD⊥PC.
在△PBC内,可求PB=PC=2
,BC=2,
在平面PBC内,作BM⊥PC,垂足为M,
设PM=x,则有8-x2=4-(2
-x)2,解得x=
<2
.
连接MD,∵PC⊥BD,BM⊥PC,BM∩BD=B,BM?平面BDM,BD?平面BDM,
∴PC⊥平面BDM.
所以满足条件的点M存在,此时PM的长为
.
∵ABCD底面ABCD为菱形,∴F为AC的中点,
又∵E为PA的中点,∴EF∥PC.
又∵EF?平面EBD,PC?平面EBD,
∴PC∥平面EBD.

(Ⅱ)解:∵底面ABCD为菱形,∠ABC=60°,
∴△ACD是边长为2正三角形,
又∵PA⊥底面ABCD,∴PA为三棱锥P-ACD的高,
∴VC-PAD=VP-ACD=
| 1 |
| 3 |
| 1 |
| 3 |
| ||
| 4 |
2
| ||
| 3 |
(Ⅲ)解:在侧棱PC上存在一点M,满足PC⊥平面MBD,下面给出证明.
∵PA⊥底面ABCD,
又ABCD底面ABCD为菱形,∴AC⊥BD,
∵BD?平面ABCD,
∴BD⊥PC.
在△PBC内,可求PB=PC=2
| 2 |
在平面PBC内,作BM⊥PC,垂足为M,
设PM=x,则有8-x2=4-(2
| 2 |
3
| ||
| 2 |
| 2 |
连接MD,∵PC⊥BD,BM⊥PC,BM∩BD=B,BM?平面BDM,BD?平面BDM,
∴PC⊥平面BDM.
所以满足条件的点M存在,此时PM的长为
3
| ||
| 2 |
点评:熟练掌握菱形的性质、三角形的中位线定理、线面平行的判定定理、线面垂直的判定与性质定理、三棱锥的体积计算公式及“等体积变形、三垂线定理是解题的关键.

练习册系列答案
相关题目
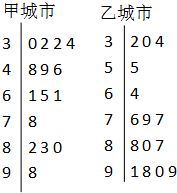 (2013•延庆县一模)空气质量指数PM2.5(单位:μg/m3)表示每立方米空气中可入肺颗粒物的含量,这个值越高,就代表空气污染越严重:
(2013•延庆县一模)空气质量指数PM2.5(单位:μg/m3)表示每立方米空气中可入肺颗粒物的含量,这个值越高,就代表空气污染越严重: