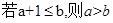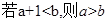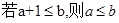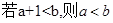题目内容
已知正四棱柱ABCD—A1B1C1D1的底面边长AB=6,侧棱长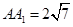 ,它的外接球的球心为O,点E是AB的中点,点P是球O的球面上任意一点,则有以下结论:
,它的外接球的球心为O,点E是AB的中点,点P是球O的球面上任意一点,则有以下结论:
①PE长的最大值是9;
②三棱锥P—EBC的最大值是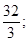 []
[]
③存在过点E的平面,截球O的截面面积是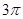 ;
;
④三棱锥P—AEC1体积的最大值是20。
其中正确结论的是 。(写出所有正确结论的序号)
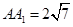 ,它的外接球的球心为O,点E是AB的中点,点P是球O的球面上任意一点,则有以下结论:
,它的外接球的球心为O,点E是AB的中点,点P是球O的球面上任意一点,则有以下结论:①PE长的最大值是9;
②三棱锥P—EBC的最大值是
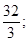 []
[]③存在过点E的平面,截球O的截面面积是
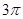 ;
;④三棱锥P—AEC1体积的最大值是20。
其中正确结论的是 。(写出所有正确结论的序号)
(1)(4)
解:(1)先求出球的半径,然后求PE的长+半径;
(2)P到平面EBC的距离+半径就是P到平面EBC的距离最大值;
(4)三棱锥P-AEC1体积的表达式,再求最大值;大圆和小圆的面积可以判断(3)的正确性.即为
由题意可知球心在体对角线的中点,直径为
半径是5,那么PE长的最大值是5+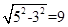 正确
正确
点P到命题 距离的最大值为5+ ,因此体积表示不正确。
,因此体积表示不正确。
球的大圆面积是25π,过E与球心连线垂直的平面是小圆,面积为9π,因而(3)是错误的.
三棱锥P-AEC1体积的最大值是V= S△AEC1•h=
S△AEC1•h= ×
× ×3×8×5=20(h最大是半径)正确.
×3×8×5=20(h最大是半径)正确.
(2)P到平面EBC的距离+半径就是P到平面EBC的距离最大值;
(4)三棱锥P-AEC1体积的表达式,再求最大值;大圆和小圆的面积可以判断(3)的正确性.即为
由题意可知球心在体对角线的中点,直径为

半径是5,那么PE长的最大值是5+
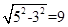 正确
正确点P到命题 距离的最大值为5+
 ,因此体积表示不正确。
,因此体积表示不正确。球的大圆面积是25π,过E与球心连线垂直的平面是小圆,面积为9π,因而(3)是错误的.
三棱锥P-AEC1体积的最大值是V=
 S△AEC1•h=
S△AEC1•h= ×
× ×3×8×5=20(h最大是半径)正确.
×3×8×5=20(h最大是半径)正确.
练习册系列答案
相关题目
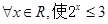 ”的否定是“
”的否定是“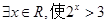 ”;
”;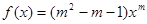 是幂函数,且在
是幂函数,且在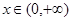 上为增函数,则
上为增函数,则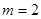 ;
;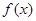 在
在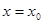 处有极值,则
处有极值,则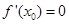 ”的否命题是真命题;
”的否命题是真命题;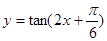 在区间
在区间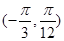 上单调递增;
上单调递增;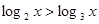 ”是“
”是“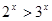 ”成立的充要条件。
”成立的充要条件。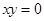 ,则
,则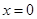 且
且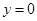 ”的逆否命题;②“正方形是菱形”的否命题;③“若
”的逆否命题;②“正方形是菱形”的否命题;③“若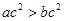 ,则
,则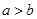 ”的逆命题;④若“
”的逆命题;④若“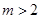 ,则不等式
,则不等式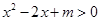 的解集为R”其中真命题为 。(写出所有真命题的序号)
的解集为R”其中真命题为 。(写出所有真命题的序号)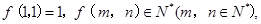 且对任何
且对任何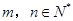 ,都有:
,都有: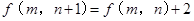 ,②
,②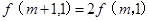 ,给出以下三个结论:(1)
,给出以下三个结论:(1)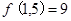 ;(2)
;(2)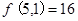 ;(3)
;(3)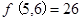 ,其中正确的是________.
,其中正确的是________.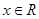 ,使得
,使得 ”的否定是
”的否定是 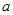 、
、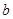 、
、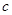 ,若
,若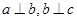 ,则
,则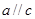 ;
;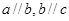 ,则
,则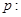 方程
方程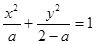 表示焦点在
表示焦点在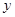 轴上的椭圆;命题
轴上的椭圆;命题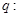 曲线
曲线 与
与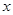 轴交于不同的两点.
轴交于不同的两点.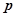 中,求a的取值范围;
中,求a的取值范围;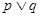 ”为真,“
”为真,“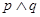 ”为假,求实数
”为假,求实数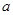 的取值范围.
的取值范围.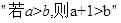 的逆否命题是
的逆否命题是