题目内容
已知从一点P引出三条射线PA、PB、PC,且两两成60°角,则二面角A-PB-C的余弦值是( )
A.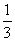 B.
B.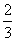 C.
C.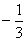 D.
D.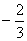
A.
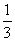 B.
B.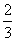 C.
C.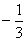 D.
D.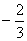
A
如图,AO⊥面BPC,由题意得:∠APB=60°,∠BPO="30°,"
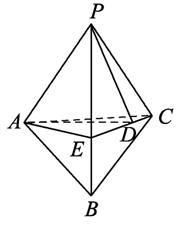
由cos∠APB=cos∠BPO·cos∠APO,即cos60°=cos30°·cos∠APO,
得cos∠APO=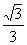 .作AE⊥PB,E为垂足,连接OE,则∠AEO就是二面角A-PB-C的平面角,不妨设PA=a,则AO=
.作AE⊥PB,E为垂足,连接OE,则∠AEO就是二面角A-PB-C的平面角,不妨设PA=a,则AO=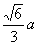 ,PO=
,PO=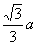 ,又在Rt△OPE中,∠OPE=30°,所以OE=
,又在Rt△OPE中,∠OPE=30°,所以OE=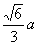 ,则在Rt△AEO中,tan∠AEO=
,则在Rt△AEO中,tan∠AEO=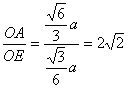 ,则cos∠AEO=
,则cos∠AEO=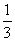 .
.
所以二面角A-PB-C的余弦值为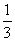 ,故选A.
,故选A.

由cos∠APB=cos∠BPO·cos∠APO,即cos60°=cos30°·cos∠APO,
得cos∠APO=
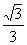 .作AE⊥PB,E为垂足,连接OE,则∠AEO就是二面角A-PB-C的平面角,不妨设PA=a,则AO=
.作AE⊥PB,E为垂足,连接OE,则∠AEO就是二面角A-PB-C的平面角,不妨设PA=a,则AO=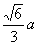 ,PO=
,PO=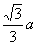 ,又在Rt△OPE中,∠OPE=30°,所以OE=
,又在Rt△OPE中,∠OPE=30°,所以OE=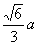 ,则在Rt△AEO中,tan∠AEO=
,则在Rt△AEO中,tan∠AEO=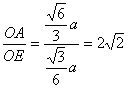 ,则cos∠AEO=
,则cos∠AEO=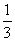 .
.所以二面角A-PB-C的余弦值为
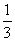 ,故选A.
,故选A.
练习册系列答案
相关题目

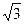 .
. SC;
SC;



 ;
; 与
与 所成角的余弦值;
所成角的余弦值; 与平面
与平面 所成二面角的平面角的余弦值为
所成二面角的平面角的余弦值为 .
.
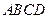 是直角梯形,角DABS是直角,
是直角梯形,角DABS是直角,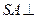 面
面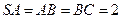 ,
,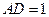 ,求面
,求面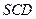 和面
和面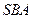 所成角的正切值.
所成角的正切值.

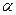 -
-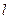 -
-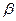 的棱
的棱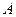 ,在平面
,在平面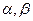 内各有一条射线
内各有一条射线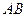 ,
,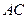 与
与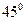 ,
,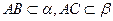 ,则
,则 。
。 与平面
与平面 相交,直线
相交,直线 是平面
是平面 ,则直线
,则直线