题目内容
在极坐标系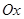 中,已知曲线
中,已知曲线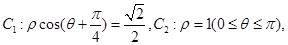
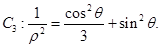 设
设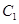 与
与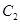 交于点
交于点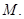
(I)求点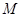 的极坐标;
的极坐标;
(II)若动直线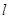 过点
过点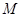 ,且与曲线
,且与曲线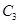 交于两个不同的点
交于两个不同的点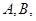 求
求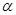
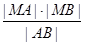 的最小值.
的最小值.
【答案】
(I)点 的极坐标为
的极坐标为
(II)当 时,
时, ,
, 有最小值
有最小值
【解析】(I)先求出曲线C1和曲线C2的普通方程,然后联立解方程组即可得到点M的直角坐标,再化成极坐标.
(II) 设直线 的参数方程为
的参数方程为 为参数),代入曲线
为参数),代入曲线 的直角坐标方程并整理得
的直角坐标方程并整理得
然后根据参数t的几何意义可知 再借助韦达定理转化为关于
再借助韦达定理转化为关于 的三角函数来求最值.
的三角函数来求最值.
解:(I)由 解得点
解得点 的直角坐标为
的直角坐标为 因此点
因此点 的极坐标为
的极坐标为
(II)设直线 的参数方程为
的参数方程为 为参数),代入曲线
为参数),代入曲线 的直角坐标方程并整理得
的直角坐标方程并整理得
设点 对应的参数分别为
对应的参数分别为 则
则 





 当
当 时,
时, ,
, 有最小值
有最小值

练习册系列答案
 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目
 A.(不等式选做题)不等式|x-1|+|x+2|<a的解集不是空集,则实数a的取值范围为
A.(不等式选做题)不等式|x-1|+|x+2|<a的解集不是空集,则实数a的取值范围为 (考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评分)
(考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评分)