题目内容
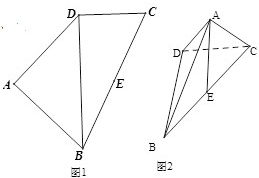 (2012•广东模拟)如图,四边形ABCD中(图1),E是BC的中点,DB=2,DC=1,BC=
(2012•广东模拟)如图,四边形ABCD中(图1),E是BC的中点,DB=2,DC=1,BC=| 5 |
| 2 |
(1)求证:AE⊥平面BDC;
(2)求异面直线AB与CD所成角的余弦值;
(3)求点B到平面ACD的距离.
分析:(1)取BD中点M,连接AM,ME.因AB=AD=
,故AM⊥BD,因 DB=2,DC=1,BC=
满足:DB2+DC2=BC2,所以△BCD是BC为斜边的直角三角形,BD⊥DC,因E是BC的中点,所以ME为△BCD的中位线ME
CD,由此能够证明AE⊥平面BDC.
(2)以M为原点MB为x轴,ME为y轴,建立空间直角坐标系由B(1,0,0),E(0,
,0),A(0,
,
),D(-1,0,0),C(-1,1,0),知
=(1,-
,-
),
=(0,-1,0),由此能法度出异面直线AB与CD所成角.
(3)由
=(-1,-
,-
),
=(0,-1,0),知
=(
,0,-2)满足,
•
=0,
•
=0,
是平面ACD的一个法向量,由此能求出点B到平面ACD的距离.
| 2 |
| 5 |
| ||
. |
| 1 |
| 2 |
(2)以M为原点MB为x轴,ME为y轴,建立空间直角坐标系由B(1,0,0),E(0,
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| AB |
| 1 |
| 2 |
| ||
| 2 |
| CD |
(3)由
| AD |
| 1 |
| 2 |
| ||
| 2 |
| CD |
| n |
| 3 |
| n |
| AD |
| n |
| CD |
| n |
解答:解:(1)如图1取BD中点M,连接AM,ME.因AB=AD=
.
∴AM⊥BD(3)…(1分)
因 DB=2,DC=1,BC=
满足:DB2+DC2=BC2,
所以△BCD是BC为斜边的直角三角形,BD⊥DC,
因E是BC的中点,所以ME为△BCD的中位线ME
CD,
∴ME⊥BD,ME=
…(2分)
∴∠AME是二面角A-BD-C的平面角,
∴∠AME=60°…(3分)
∵AM⊥BD,ME⊥BD且AM、ME是平面AME内两相交于M的直线
∴BD⊥平面AEM∵AE?平面AEM,
∴BD⊥AE…(4分)
因AB=AD=
.,DB=2,
∴△ABD为等腰直角三角形,
∴AM=
BD=1,AE2=AM2+ME2-2AM•ME•cos∠AME=1+
-2×1×
×cos60°=
∴AE=
∴AE2+ME2=1=AM2,
∴AE⊥ME…(6分)
∴BD∩ME,BD?面BDC,ME?面BDC,
∴AE⊥平面BDC…(7分)
(2)如图2,以M为原点MB为x轴,ME为y轴,建立空间直角坐标系,(8分)
则由(1)及已知条件可知B(1,0,0),E(0,
,0),A(0,
,
),
D(-1,0,0),C(-1,1,0),
=(1,-
,-
),
=(0,-1,0),…(9分)
设异面直线AB与CD所成角为θ,
则cosθ=|
|…(10分)
=
=
.…(11分)
(3)由
=(-1,-
,-
),
=(0,-1,0),
可知
=(
,0,-2)满足,
•
=0,
•
=0,
是平面ACD的一个法向量,…(12分)
记点B到平面ACD的距离d,
则
在法向量
方向上的投影绝对值为d
则d=|
|…(13分),
所以d=|
|=
…(14分)
| 2 |
∴AM⊥BD(3)…(1分)
因 DB=2,DC=1,BC=
| 5 |
所以△BCD是BC为斜边的直角三角形,BD⊥DC,
因E是BC的中点,所以ME为△BCD的中位线ME
| ||
. |
| 1 |
| 2 |
∴ME⊥BD,ME=
| 1 |
| 2 |
∴∠AME是二面角A-BD-C的平面角,
∴∠AME=60°…(3分)
∵AM⊥BD,ME⊥BD且AM、ME是平面AME内两相交于M的直线
∴BD⊥平面AEM∵AE?平面AEM,
∴BD⊥AE…(4分)
因AB=AD=
| 2 |
∴△ABD为等腰直角三角形,
∴AM=
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
| 3 |
| 4 |
| ||
| 2 |
∴AE2+ME2=1=AM2,
∴AE⊥ME…(6分)
∴BD∩ME,BD?面BDC,ME?面BDC,
∴AE⊥平面BDC…(7分)
(2)如图2,以M为原点MB为x轴,ME为y轴,建立空间直角坐标系,(8分)
则由(1)及已知条件可知B(1,0,0),E(0,
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
D(-1,0,0),C(-1,1,0),
| AB |
| 1 |
| 2 |
| ||
| 2 |
| CD |
设异面直线AB与CD所成角为θ,
则cosθ=|
| ||||
|
=
| ||
|
| ||
| 4 |
(3)由
| AD |
| 1 |
| 2 |
| ||
| 2 |
| CD |
可知
| n |
| 3 |
| n |
| AD |
| n |
| CD |
| n |
记点B到平面ACD的距离d,
则
| AB |
| n |
则d=|
| ||||
|
|
所以d=|
| ||||
|
2
| ||
| 7 |
点评:本题考查直线和平面垂直的证明,求异面直线与直线所成角的余弦值,求点到平面的距离.解题时要认真审题,仔细解答,注意合理地进行等价转化.

练习册系列答案
相关题目
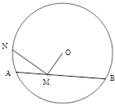 (2012•广东模拟)(几何证明选讲选做题)如图,点M为⊙O的弦AB上的一点,连接MO.MN⊥OM,MN交圆于N,若MA=2,MB=4,则MN=
(2012•广东模拟)(几何证明选讲选做题)如图,点M为⊙O的弦AB上的一点,连接MO.MN⊥OM,MN交圆于N,若MA=2,MB=4,则MN=