题目内容
(2012•广东模拟)甲、乙两人各射击一次,击中目标的概率分别是
和
假设两人射击是否击中目标,相互之间没有影响;每人各次射击是否击中目标,相互之间也没有影响.
(1)求甲射击3次,至少1次未击中目标的概率;
(2)假设某人连续2次未击中目标,则停止射击,问:乙恰好射击4次后,被中止射击的概率是多少?
(3)设甲连续射击3次,用ξ表示甲击中目标时射击的次数,求ξ的数学期望Eξ.(结果可以用分数表示)
| 2 |
| 3 |
| 3 |
| 4 |
(1)求甲射击3次,至少1次未击中目标的概率;
(2)假设某人连续2次未击中目标,则停止射击,问:乙恰好射击4次后,被中止射击的概率是多少?
(3)设甲连续射击3次,用ξ表示甲击中目标时射击的次数,求ξ的数学期望Eξ.(结果可以用分数表示)
分析:(1)求甲射击3次,至少1次未击中目标的概率,考虑其对立事件的概率即可;
(2)设“乙恰好射击5次后,被中止射击”为事件C,根据题意,必然乙是最后两次未击中目标,第一次及第二次至多次有一次未击中目标,结合概率的计算公式,计算可得答案;
(3)ξ服从二项分布,根据期望公式即可求得,或者先求分布列,再求期望.
(2)设“乙恰好射击5次后,被中止射击”为事件C,根据题意,必然乙是最后两次未击中目标,第一次及第二次至多次有一次未击中目标,结合概率的计算公式,计算可得答案;
(3)ξ服从二项分布,根据期望公式即可求得,或者先求分布列,再求期望.
解答:解:(1)记“甲连续射击3次,至少1次未击中目标”为事件A1,由题意,射击3次,相当于3次独立重复试验,故P(A1)=1-P(
)=1-(
)3=
答:甲射击3次,至少1次未击中目标的概率为
;…(4分)
(2)记“乙恰好射击4次后,被中止射击”为事件A2,由于各事件相互独立,
故P(A2)=
×
×
×
+
×
×
×
=
,
答:乙恰好射击4次后,被中止射击的概率是
…(8分)
(3)根据题意ξ服从二项分布,Eξ=3×
=2…(12分)
(3)方法二:p(ξ=0)=
•(
)3=
p(ξ=1)=
•(
)•(
)2=
p(ξ=2)=
•(
)2•(
)1=
p(ξ=1)=
•(
)3•(
)0=
∴Eξ=0×
+1×
+2×
+3×
=2…(12分)
说明:(1),(2)两问没有文字说明分别扣(1分),没有答,分别扣(1分).
第(3)问方法对,算错数的扣(2分)
. |
| A1 |
| 2 |
| 3 |
| 19 |
| 27 |
| ξ | 0 | 1 | 2 | 3 | ||||||||
| p |
|
|
|
|
| 19 |
| 27 |
(2)记“乙恰好射击4次后,被中止射击”为事件A2,由于各事件相互独立,
故P(A2)=
| 1 |
| 4 |
| 1 |
| 4 |
| 3 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
| 64 |
答:乙恰好射击4次后,被中止射击的概率是
| 3 |
| 64 |
(3)根据题意ξ服从二项分布,Eξ=3×
| 2 |
| 3 |
(3)方法二:p(ξ=0)=
| C | 0 3 |
| 1 |
| 3 |
| 1 |
| 27 |
| C | 1 3 |
| 2 |
| 3 |
| 1 |
| 3 |
| 6 |
| 27 |
| C | 2 3 |
| 2 |
| 3 |
| 1 |
| 3 |
| 12 |
| 27 |
| C | 3 3 |
| 2 |
| 3 |
| 1 |
| 3 |
| 8 |
| 27 |
∴Eξ=0×
| 1 |
| 27 |
| 6 |
| 27 |
| 12 |
| 27 |
| 8 |
| 27 |
说明:(1),(2)两问没有文字说明分别扣(1分),没有答,分别扣(1分).
第(3)问方法对,算错数的扣(2分)
点评:本题考查相互独立事件的概率的乘法公式与n次重复试验中恰有k次发生的概率,考查随机变量的期望,解题的关键是明确事件之间的相互关系(互斥、对立等).

练习册系列答案
相关题目
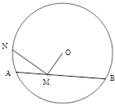 (2012•广东模拟)(几何证明选讲选做题)如图,点M为⊙O的弦AB上的一点,连接MO.MN⊥OM,MN交圆于N,若MA=2,MB=4,则MN=
(2012•广东模拟)(几何证明选讲选做题)如图,点M为⊙O的弦AB上的一点,连接MO.MN⊥OM,MN交圆于N,若MA=2,MB=4,则MN=