题目内容
（本小题满分14分）
已知向量
，
，函数
．
(1)求函数
的解析式；
(2)当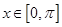
时，求的单调递增区间；
(3)说明的图象可以由
的图象经过怎样的变换而得到．
(1) 
；
(2) 
和
；(3)见解析
解析
练习册系列答案
轻松暑假总复习系列答案
相关题目
轻松暑假总复习系列答案题目内容
（本小题满分14分）
已知向量，，函数．
(1)求函数的解析式；
(2)当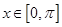时，求的单调递增区间；
(3)说明的图象可以由的图象经过怎样的变换而得到．
(1) ；
(2) 和；(3)见解析
解析
轻松暑假总复习系列答案
的终边上有一点
，求
的值；
的值。
．
的单调递增区间；
，
，求
的值． 
.向量
.
时,求函数
的值域;
时,求函数
，弧长为
，求该扇形的圆心角（用弧度制表示）；
的终边在直线
上，求
的值.
（
）的部分图像， 
是这部分图象与
轴的交点（按图所示），函数图象上的点
满足：
.
的周期；
的横坐标为1，试求函数
的解析式，并求
的值. 
在区间［
］上的最大值为6，
关于y轴的对称图象得函数
的图象，再把
个单位得
的图象，求函数
。
的最小正周期和单调递减区间；
，是否存在实数m，使函数
的值域恰为
？若存在，请求出m的
，函数
，
时，
,求常数
，
的值.