题目内容
7.有下列说法:①曲线的切线与曲线有且只有一个公共点:②曲线上任意一点都可以用割线逼近切线的方法作出过此点的切线:
③曲线在点P附近经过放大后可以近似的看成直线,则曲线在点P处一定存在切线;
④以曲线上某点为切点的曲线的切线可以作出两条.
其中,正确的是③(填序号)
分析 由高次函数所对应的曲线在某点处的切线可能与曲线交于另外的点说明①错误;
由函数在不可导位置不存在切线说明②错误;
曲线在点P附近经过放大后可以近似的看成直线,则曲线在点P处一定存在切线,正确;
若曲线在某点处存在切线,切线唯一说明④错误.
解答 解:①曲线的切线与曲线有且只有一个公共点,错误,可能有多个交点;
②曲线上任意一点都可以用割线逼近切线的方法作出过此点的切线,错误,对于不可导的位置,是不存在切线的;
③曲线在点P附近经过放大后可以近似的看成直线,则曲线在点P处一定存在切线,正确;
④以曲线上某点为切点的曲线的切线可以作出两条,错误,最多能作一条.
∴正确的命题是③.
故答案为:③.
点评 本题考查命题的真假判断与应用,考查了曲线的方程与方程的曲线的概念,考查过曲线上某点的切线问题,是中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
18.若一元二次不等式x2-$\frac{2}{\sqrt{a}}$x+1-$\frac{1}{b}$>0(b>a)的解集为{x|x≠$\frac{1}{\sqrt{a}}$},则$\frac{4}{a-1}$+$\frac{16}{b-1}$的最小值为( )
| A. | 16 | B. | 25 | C. | 36 | D. | 49 |
16.已知O为坐标原点,实数x,y满足$\left\{\begin{array}{l}{x-y+1≤0}\\{3x+4y≤12}\\{x-1≥0}\end{array}\right.$,P(x,y)为该不等式组所表示的平面区域内任意一点,使z=x+2y取最大值的点为A点,则|OP|•|AO|•cos∠AOP的最大值等于( )
| A. | $\frac{97}{16}$ | B. | $\frac{11}{2}$ | C. | $\frac{167}{28}$ | D. | $\frac{38}{7}$ |
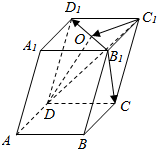 如图,在平行六面体ABCD-A1B1C1D1中,O是B1D1的中点,求证:B1C∥平面ODC1.
如图,在平行六面体ABCD-A1B1C1D1中,O是B1D1的中点,求证:B1C∥平面ODC1.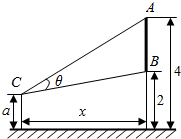 如图,墙上有一壁画,最高点A离地面4米,最低点B离地面2米.观察者从距离墙x(x>1)米,离地面高a(1≤a≤2)米的C处观赏该壁画,设观赏视角∠ACB=θ.
如图,墙上有一壁画,最高点A离地面4米,最低点B离地面2米.观察者从距离墙x(x>1)米,离地面高a(1≤a≤2)米的C处观赏该壁画,设观赏视角∠ACB=θ.