题目内容
20.已知k∈R,函数f(x)=lnx-kx.(Ⅰ)若k>0,求函数f(x)的单调区间;
(Ⅱ)若f(x)有两个相异的零点x1,x2,求证:x1•x2>e2.
分析 (Ⅰ)对f′(x)=$\frac{1-kx}{x}(x>0)$求出函数的单调区间即可
(Ⅱ)要证x1x2>e2即证lnx1+lnx2>2?k(x1+x2)>2,构造新函数,利用新函数的导数求出单调区间即可得出结论.
解答 解:(Ⅰ)f′(x)=$\frac{1-kx}{x}(x>0)$在(0,$\frac{1}{k}$)上f'(x)>0,f(x)单调递增,在($\frac{1}{k},+∞$)上f'(x)<0,f(x)单调递减;
(Ⅱ)证明:设0<x1<x2,f(x1)=f(x2)=0,
lnx1-kx1=lnx2-kx2=0,
要证x1x2>e2即证lnx1+lnx2>2?k(x1+x2)>2?$k>\frac{2}{{x}_{1}+{x}_{2}}$?$\frac{ln{x}_{1}-ln{x}_{2}}{{x}_{1}-{x}_{2}}>\frac{2}{{x}_{1}-{x}_{2}}$?$\frac{{x}_{2}}{{x}_{1}}$$>\frac{2({x}_{2}-{x}_{1})}{{x}_{1}+{x}_{2}}$
令$\frac{{x}_{2}}{x1}=t$,则t>1,$\frac{{x}_{2}}{{x}_{1}}$$>\frac{2({x}_{2}-{x}_{1})}{{x}_{1}+{x}_{2}}$?$lnt>\frac{2(t-1)}{t+1}$
令g(t)=lnt-$\frac{2(t-1)}{t+1}(t>1)$
g'(t)=$\frac{(t-1)^{2}}{t(t+1)^{2}}>0$,所以g(t)在(1,+∞)上单调递增,
故g(t)>g(1)=0,即$lnt>\frac{2(t-1)}{t+1}$成立,∴${x}_{1}{x}_{2}>{e}^{2}$成立.
点评 本题主要考查导数在求函数单调区间中的应用和利用导数证明不等似的成立,属于中档题型,在高考中时有涉及.

 教材全解字词句篇系列答案
教材全解字词句篇系列答案| A. | 12 | B. | 24 | C. | 36 | D. | 48 |
| A. | 12 | B. | 14 | C. | 6 | D. | 7 |
| A. | 540 | B. | 480 | C. | 360 | D. | 200 |
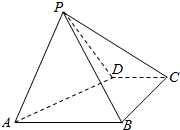 如图,四棱锥P-ABCD中,底面ABCD是直角梯形,AB∥CD,∠DAB=60°,AB=AD=2CD=2,侧面PAD⊥底面ABCD,且△PAD 是以AD为底的等腰三角形.
如图,四棱锥P-ABCD中,底面ABCD是直角梯形,AB∥CD,∠DAB=60°,AB=AD=2CD=2,侧面PAD⊥底面ABCD,且△PAD 是以AD为底的等腰三角形.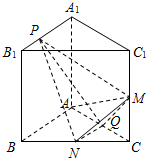 如图,已知直三棱柱ABC-A1B1C1中,AA1=AB=AC,AB⊥AC,M,N,Q分别是CC1,BC,AC的中点,点P在线段A1B1上运动.
如图,已知直三棱柱ABC-A1B1C1中,AA1=AB=AC,AB⊥AC,M,N,Q分别是CC1,BC,AC的中点,点P在线段A1B1上运动.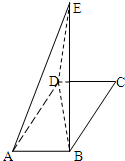 如图,在平行四边形ABCD中∠DAB=60°AB=2,AD=4,将△ABC沿BD折起到△EBD的位置.
如图,在平行四边形ABCD中∠DAB=60°AB=2,AD=4,将△ABC沿BD折起到△EBD的位置.