题目内容
一个袋子中装有7个小球,其中红球4个,编号分别为1,2,3,4,黄球3个,编号分别为2,4,6,从袋子中任取4个小球(假设取到任一小球的可能性相等).
(1)求取出的小球中有相同编号的概率;
(2)记取出的小球的最大编号为 ,求随机变量
,求随机变量 的分布列和数学期望.
的分布列和数学期望.
(1)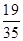 ;
;
(2)随机变量 的分布列为:
的分布列为:
随机变量
3 4 6 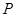
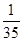
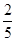
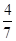
 的数学期望
的数学期望 .
.
解析试题分析:(1)应用古典概型概率的计算公式,关键是利用组合知识,确定事件数;
(2) 随机变量 的可能取值为
的可能取值为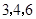 .
.
计算相应概率即得随机变量 的分布列为:
的分布列为:
数学期望
3 4 6 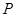
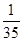
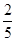
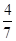
 .
.
试题解析:(1):设取出的小球中有相同编号的事件为 ,
,
编号相同可分成一个相同和两个相同 2分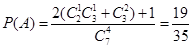 4分
4分
(2) 随机变量 的可能取值为:3,4,6 6分
的可能取值为:3,4,6 6分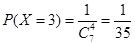 , 7分
, 7分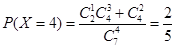 , 8分
, 8分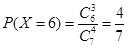 9分
9分
所以随机变量 的分布列为:
的分布列为:
10分
3 4 6 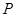
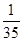
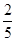
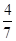
所以随机变量 的数学期望
的数学期望 . &
. &

练习册系列答案
相关题目
甲、乙两运动员进行射击训练,已知他们击中目标的环数都稳定在7,8,9,10环,且每次射击成绩互不影响,射击环数的频率分布表如下:
甲运动员
| 射击环数 | 频数 | 频率 |
| 7 | 10 | 0.1 |
| 8 | 10 | 0.1 |
| 9 | x | 0.45 |
| 10 | 35 | y |
| 合计 | 100 | 1 |
| 射击环数 | 频数 | 频率 |
| 7 | 8 | 0.1 |
| 8 | 12 | 0.15 |
| 9 | z | |
| 10 | | 0.35 |
| 合计 | 80 | 1 |
(1)求甲运动员射击1次击中10环的概率.
(2)求甲运动员在3次射击中至少有1次击中9环以上(含9环)的概率.
(3)若甲运动员射击2次,乙运动员射击1次,ξ表示这3次射击中击中9环以上(含9环)的次数,求ξ的分布列及E(ξ).
某产品的三个质量指标分别为x,y,z,用综合指标S=x+y+z评价该产品的等级.若S≤4,则该产品为一等品.现从一批该产品中,随机抽取10件产品作为样本,其质量指标列表如下:
| 产品编号 | A1 | A2 | A3 | A4 | A5 |
| 质量指标(x,y,z) | (1,1,2) | (2,1,1) | (2,2,2) | (1,1,1) | (1,2,1) |
| | | | | | |
| 产品编号 | A6 | A7 | A8 | A9 | A10 |
| 质量指标(x,y,z) | (1,2,2) | (2,1,1) | (2,2,1) | (1,1,1) | (2,1,2) |
(2)在该样本的一等品中,随机抽取2件产品,
①用产品编号列出所有可能的结果;
②设事件B为“在取出的2件产品中,每件产品的综合指标S都等于4”,求事件B发生的概率.
 ,x∈(-∞,+∞),试求光通量在下列范围内的灯泡的个数.
,x∈(-∞,+∞),试求光通量在下列范围内的灯泡的个数. ,除以3的余数为
,除以3的余数为
 为事件
为事件 ,事件
,事件 为事件
为事件 ,判断事件
,判断事件
 ,乙在每局中获胜的概率为
,乙在每局中获胜的概率为 ,且各局胜负相互独立,比赛停止时一共已打
,且各局胜负相互独立,比赛停止时一共已打 局:
局: