题目内容
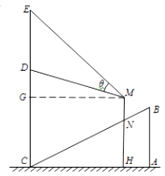
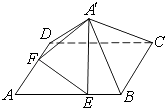
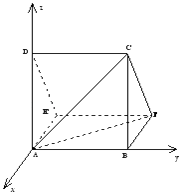
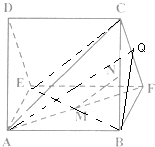
【题目】一个多面体的直观图(图1)及三视图(图2)如图所示,其中M,N分别是AF,BC的中点 
(1)求证:MN∥平面CDEF:
(2)求二面角A﹣CF﹣B的余弦值;
【答案】
(1)证明:由三视图知,
该多面体是底面为直角三角形的直三棱柱ADE﹣BCF,
且AB=BC=BF=4,DE=CF= ![]() ,∠CBF=90°,
,∠CBF=90°,
连结BE,M在BE上,连结CE
EM=BM,CN=BN,所以MN∥CE,CE面CDEF,
所以MN∥平面CDEF.
(2)解法一:作BQ⊥CF于Q,连结AQ,
面BFC⊥面ABFE,面ABFE∩面BFC=BF,
AB面ABFE,AB⊥BF,
∴AB⊥面BCF,
CF面BCF,∴AB⊥CF,BQ⊥CF,AB∩BQ=B,
∴CF⊥面ABQ,AQ面ABQ,
AQ⊥CF,∴∠AQB为所求的二面角的平面角,
在Rt△ABQ中,tan∠AQB= ![]() =
= ![]() =
= ![]() ,
,
∴cos ![]() ,
,
∴二面角A﹣CF﹣B的余弦值为 ![]() .
.
解法二:以EA,AB,AD所在直线为x轴,y轴,z轴,
建立空间直角坐标系,
A(0,0,0),B(0,4,0),C(0,4,4),F(﹣4,4,0),
面CBF法向量为 ![]() ,
,
![]() ,
,
设面ACF法向量为 ![]() ,
,
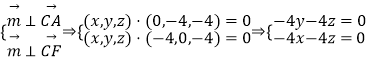
取z=﹣1,所以 ![]()
设二面角为θ,
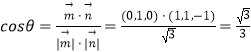 ,
,
∴二面角A﹣CF﹣B的余弦值为 ![]() .
.
【解析】(Ⅰ)由三视图知,该多面体是底面为直角三角形的直三棱柱ADE﹣BCF,且AB=BC=BF=4,DE=CF= ![]() ,∠CBF=90°,由此能证明MN∥平面CDEF.(Ⅱ)(法一)作BQ⊥CF于Q,连结AQ,由已知得AB⊥面BCF,AB⊥CF,BQ⊥CF,∠AQB为所求的二面角的平面角,由此能求出二面角A﹣CF﹣B的余弦值.(Ⅱ)(法二):以EA,AB,AD所在直线为x轴,y轴,z轴,建立空间直角坐标系,利用向量法能求出二面角A﹣CF﹣B的余弦值.
,∠CBF=90°,由此能证明MN∥平面CDEF.(Ⅱ)(法一)作BQ⊥CF于Q,连结AQ,由已知得AB⊥面BCF,AB⊥CF,BQ⊥CF,∠AQB为所求的二面角的平面角,由此能求出二面角A﹣CF﹣B的余弦值.(Ⅱ)(法二):以EA,AB,AD所在直线为x轴,y轴,z轴,建立空间直角坐标系,利用向量法能求出二面角A﹣CF﹣B的余弦值.
【考点精析】解答此题的关键在于理解直线与平面平行的判定的相关知识,掌握平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行.