题目内容
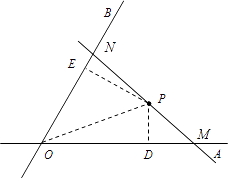
【题目】如图,OA、OB是两条公路(近似看成两条直线), ![]() ,在∠AOB内有一纪念塔P(大小忽略不计),已知P到直线OA、OB的距离分别为PD、PE,PD=6千米,PE=12千米.现经过纪念塔P修建一条直线型小路,与两条公路OA、OB分别交于点M、N.
,在∠AOB内有一纪念塔P(大小忽略不计),已知P到直线OA、OB的距离分别为PD、PE,PD=6千米,PE=12千米.现经过纪念塔P修建一条直线型小路,与两条公路OA、OB分别交于点M、N. 
(1)求纪念塔P到两条公路交点O处的距离;
(2)若纪念塔P为小路MN的中点,求小路MN的长.
【答案】
(1)解:设∠POA=α,则 ![]() ,
,
∵PD=6,PE=12,
∴ ![]() ,
,
∴ ![]() ,化简得
,化简得 ![]() ,
,
又sin2α+cos2α=1,∴ ![]() ,
,
∴ ![]() .
.
∴纪念塔P到两条公路交点O处的距离为4 ![]() 千米
千米
(2)解:设∠PMO=θ,则∠PNO= ![]() ﹣θ,
﹣θ,
∵P为MN的中点,即PM=PN,
∴ ![]() ,
,
即 ![]() ,解得
,解得 ![]() ,
,
∴ ![]() .
.
∴小路MN的长为24千米.
【解析】(1)设∠POA=α,分别在△OPD和△OPE中用α表示出OP,解方程即可得出α,从而求出OP的长;(2)设∠PMO=θ,分别表示出PM,PN,解方程得出θ,从而得出MN的长.

练习册系列答案
相关题目



