题目内容
平行四边形ABCD的顶点的坐标分别为A(-1,-4),B(3,-2),D(-3,4),则顶点C的坐标为 ________,两对角线交点M的坐标 ________.
(1,6) (0,1)
分析:根据平行四边形的性质可得AB平行于CD,AD平行于BC,利用两直线平行时斜率相等分别求出直线AB和直线BC的斜率即可得到直线CD和直线AD的斜率,分别写出直线CD和直线AD的方程,联立即可求出交点C的坐标,再根据平行四边形的性质对角线互相平分得到M为AC的中点,根据中点坐标公式求出即可.
解答:根据平行四边形的性质可知AB∥CD,得到kCD=kAB=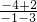 =
= ,所以直线CD的方程为y-4=
,所以直线CD的方程为y-4= (x+3)①;
(x+3)①;
同理AD∥BC,得到kBC=kAD=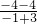 =-4,所以直线AD的方程为y-4=-4(x-3)②
=-4,所以直线AD的方程为y-4=-4(x-3)②
联立①②解得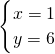 ,所以顶点C的坐标为(1,6);
,所以顶点C的坐标为(1,6);
根据平行四边形的性质可得对角线的交点M为AC的中点,所以M(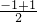 ,
,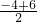 )=(0,1).
)=(0,1).
故答案为:(1,6),(0,1)
点评:此题考查学生灵活运用平行四边形的性质,掌握两直线平行时斜率的关系,会根据一点和斜率写出直线的方程,灵活运用中点坐标公式求值,是一道中档题.
分析:根据平行四边形的性质可得AB平行于CD,AD平行于BC,利用两直线平行时斜率相等分别求出直线AB和直线BC的斜率即可得到直线CD和直线AD的斜率,分别写出直线CD和直线AD的方程,联立即可求出交点C的坐标,再根据平行四边形的性质对角线互相平分得到M为AC的中点,根据中点坐标公式求出即可.
解答:根据平行四边形的性质可知AB∥CD,得到kCD=kAB=
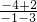 =
= ,所以直线CD的方程为y-4=
,所以直线CD的方程为y-4= (x+3)①;
(x+3)①;同理AD∥BC,得到kBC=kAD=
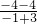 =-4,所以直线AD的方程为y-4=-4(x-3)②
=-4,所以直线AD的方程为y-4=-4(x-3)②联立①②解得
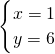 ,所以顶点C的坐标为(1,6);
,所以顶点C的坐标为(1,6);根据平行四边形的性质可得对角线的交点M为AC的中点,所以M(
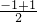 ,
,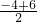 )=(0,1).
)=(0,1).故答案为:(1,6),(0,1)
点评:此题考查学生灵活运用平行四边形的性质,掌握两直线平行时斜率的关系,会根据一点和斜率写出直线的方程,灵活运用中点坐标公式求值,是一道中档题.

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目