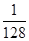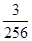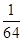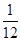题目内容
据民生所望,相关部门对所属服务单位进行整治行核查,规定:从甲类3个指标项中随机抽取2项,从乙类2个指标项中随机抽取1项.在所抽查的3个指标项中,3项都优秀的奖励10万元;只有甲类2项优秀的奖励6万元;甲类只有1项优秀、乙类1项优秀的提出警告,有2项或2项以上不优秀的停业运营并罚款8万元.已知某家服务单位甲类3项指标项中有2项优秀,乙类2项指标项中有1项优秀.
求:(1)这家单位受到奖励的概率;
(2)这家单位这次整治性核查中所获金额的均值(奖励为正数,罚款为负数).
求:(1)这家单位受到奖励的概率;
(2)这家单位这次整治性核查中所获金额的均值(奖励为正数,罚款为负数).
(1)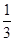 ;(2)均值为0元.
;(2)均值为0元.
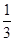 ;(2)均值为0元.
;(2)均值为0元.试题分析:本题主要考查古典概型的概率和均值等基础知识,考查综合分析问题解决问题的能力,考查运用概率知识解决简单实际问题的能力,考查计算能力.第一问,由题意分析可知,受到奖励的有10万元和6万元2种情况,即所抽查的3个指标项都优秀和只有甲类2项优秀的情况,先把甲和乙中的指标项设出字母,把取3项的所有情况全部列出来共6种情况,在这6种情况中选出上述符合题意的情况,写出概率值;第二问,分别求出10万元,6万元,0万元,-8万元的情况种数,求出均值.
试题解析:记这家单位甲类优秀的指标项为
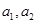 ,甲类非优秀的指标项为
,甲类非优秀的指标项为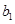 ;乙类优秀的指标项为
;乙类优秀的指标项为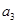 ,乙类非优秀的指标项为
,乙类非优秀的指标项为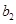 .依题意,被抽取的指标项的可能结果有:
.依题意,被抽取的指标项的可能结果有: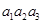 ,
,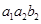 ,
,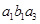 ,
,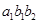 ,
,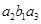 ,
,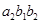 共6种.
共6种.(Ⅰ)记这家公司“获得10万元奖励”为事件
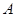 ,“获得6万元奖励”为事件
,“获得6万元奖励”为事件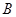 ,则
,则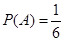 ,
,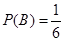 . 7分
. 7分记这家公司“获奖”为事件C,则
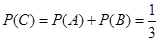 .
.(Ⅱ)这家单位这次整治性核查中所获金额的均值为
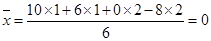 (万元).
(万元).
练习册系列答案
相关题目
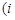 ,
,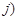 表示甲乙抽到的牌的数字,
表示甲乙抽到的牌的数字,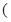 如甲抽到红桃2,乙抽到红桃3,记为
如甲抽到红桃2,乙抽到红桃3,记为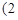 ,
, ,写出甲乙二人抽到的牌的所有情况;
,写出甲乙二人抽到的牌的所有情况;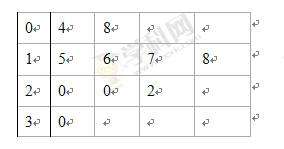
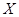 ,求随机变量
,求随机变量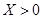 就去打球;若
就去打球;若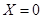 就去唱歌;若
就去唱歌;若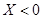 就去下棋.
就去下棋.