题目内容
小波以游戏方式决定:是去打球、唱歌还是去下棋.游戏规则为:以O为起点,再从A1,A2,A3,A4,A5,A6(如图)这6个点中任取两点分别为终点得到两个向量,记这两个向量的数量积为X,若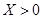 就去打球;若
就去打球;若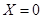 就去唱歌;若
就去唱歌;若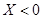 就去下棋.
就去下棋.
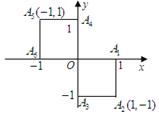
(Ⅰ)写出数量积X的所有可能取值;
(Ⅱ)分别求小波去下棋的概率和不去唱歌的概率.
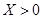 就去打球;若
就去打球;若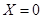 就去唱歌;若
就去唱歌;若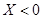 就去下棋.
就去下棋.
(Ⅰ)写出数量积X的所有可能取值;
(Ⅱ)分别求小波去下棋的概率和不去唱歌的概率.
(Ⅰ)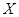 的所有可能取值为
的所有可能取值为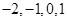 ;(Ⅱ)小波去下棋的概率为
;(Ⅱ)小波去下棋的概率为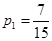 ,小波不去唱歌的概率
,小波不去唱歌的概率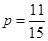 .
.
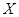 的所有可能取值为
的所有可能取值为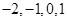 ;(Ⅱ)小波去下棋的概率为
;(Ⅱ)小波去下棋的概率为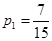 ,小波不去唱歌的概率
,小波不去唱歌的概率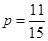 .
.试题分析:(Ⅰ)
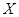 的所有可能取值,即从
的所有可能取值,即从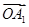 ,
,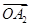 ,
,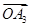 ,
,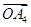 ,
,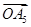 ,
,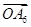 这六个向量中任取两个,共有
这六个向量中任取两个,共有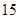 种,
种,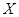 的所有可能取值为
的所有可能取值为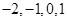 ;(Ⅱ)数量积为-2的只有一种,数量积为-1的有六种,数量积为0的有四种,数量积为1的有四种,故所有可能的情况共有15种,利用古典概型概率公式计算.
;(Ⅱ)数量积为-2的只有一种,数量积为-1的有六种,数量积为0的有四种,数量积为1的有四种,故所有可能的情况共有15种,利用古典概型概率公式计算.试题解析:(Ⅰ)
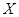 的所有可能取值,即从
的所有可能取值,即从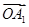 ,
,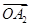 ,
,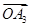 ,
,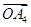 ,
,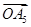 ,
,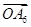
这六个向量中任取两个,共有
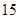 种。 2分
种。 2分由下表可知
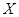 的所有可能取值为
的所有可能取值为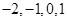 ;故
;故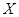 的所有可能取值为
的所有可能取值为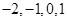 ; 6分
; 6分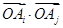 | 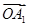 | 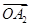 | 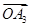 | 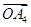 | 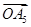 | 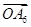 |
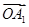 | | 1 | 0 | 0 | -1 | -1 |
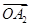 | | | 1 | -1 | -2 | -1 |
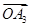 | | | | -1 | -1 | 0 |
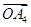 | | | | | 1 | 0 |
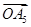 | | | | | | 1 |
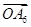 | | | | | | |
所以小波去下棋的概率为
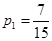 . 10分
. 10分因为去唱歌的概率为
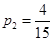 ,所以小波不去唱歌的概率
,所以小波不去唱歌的概率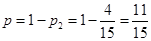 .12分
.12分
练习册系列答案
相关题目
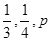 ,
,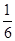 .
.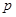 的值,
的值,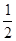
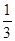
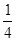
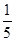
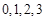 中任意取出两个不同的数,其和为3的概率是________ .
中任意取出两个不同的数,其和为3的概率是________ .