题目内容
一个盒子中装有形状大小相同的5张卡片,上面分别标有数字1,2,3,4,5,甲乙两人分别从盒子中随机不放回的各抽取一张.
(Ⅰ)写出所有可能的结果,并求出甲乙所抽卡片上的数字之和为偶数的概率;
(Ⅱ)以盒子中剩下的三张卡片上的数字作为边长来构造三角形,求出能构成三角形的概率.
(Ⅰ)写出所有可能的结果,并求出甲乙所抽卡片上的数字之和为偶数的概率;
(Ⅱ)以盒子中剩下的三张卡片上的数字作为边长来构造三角形,求出能构成三角形的概率.
(Ⅰ)甲乙两人分别从盒子中随机不放回的各抽取一张,基本事件有
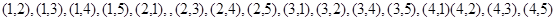
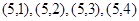 共20个;
共20个;
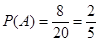 .
.
(Ⅱ)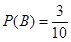 .
.
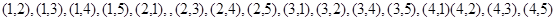
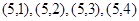 共20个;
共20个;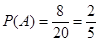 .
.(Ⅱ)
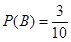 .
.试题分析:(Ⅰ)借助于“树图法”可得基本事件有:
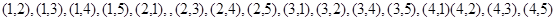
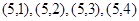 共20个
共20个设事件
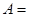 “甲乙所抽卡片上的数字之和为偶数”
“甲乙所抽卡片上的数字之和为偶数”其中甲乙所抽卡片上的数字之和为偶数的有:
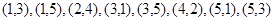 共8个,利用概率计算公式计算.
共8个,利用概率计算公式计算.(Ⅱ)剩下的三边长包含的基本事件为:
 共10个;
共10个;其中“剩下的三张卡片上的数字作为边长能构成三角形”的有:
 共3个.
共3个.解答此类问题,关键是计算正确“事件数”,“列表法”“树图法”“坐标法”等,是常用方法.
试题解析:(Ⅰ)甲乙两人分别从盒子中随机不放回的各抽取一张,基本事件有
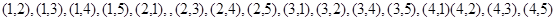
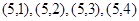 共20个 2分
共20个 2分设事件
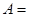 “甲乙所抽卡片上的数字之和为偶数”
“甲乙所抽卡片上的数字之和为偶数”则事件
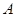 包含的基本事件有
包含的基本事件有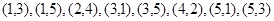 共8个 4分
共8个 4分所以
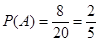 . 6分
. 6分(Ⅱ)剩下的三边长包含的基本事件为:
 共10个; 8分
共10个; 8分设事件
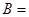 “剩下的三张卡片上的数字作为边长能构成三角形“
“剩下的三张卡片上的数字作为边长能构成三角形“则事件
 包含的基本事件有:
包含的基本事件有: 共3个 10分
共3个 10分所以
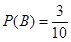 . 12分
. 12分备注:第二问也可看做20个基本事件,重复一倍。

练习册系列答案
 百年学典课时学练测系列答案
百年学典课时学练测系列答案
相关题目
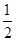 ,记政治、历史、地理达到优秀水平的事件分别为
,记政治、历史、地理达到优秀水平的事件分别为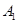 、
、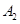 、
、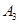 ,未达到优秀水平的事件分别为
,未达到优秀水平的事件分别为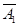 、
、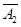 、
、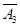 .
.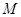 ,试求事件
,试求事件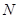 ,使得事件
,使得事件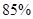 ,并说明理由.
,并说明理由.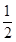
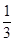
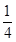
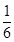
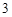 人中随机选派
人中随机选派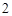 人参加某项活动,则甲被选中的概率为 .
人参加某项活动,则甲被选中的概率为 .