Question

11．点P（a，b）在以A（-4，1），B（-1，0），C（-2，0）为顶点的△ABC的内部运动（不包含边界），则$\frac{a-1}{2b-4}$的取值范围是（$\frac{1}{2}$，$\frac{5}{2}$）．

Answer 1

分析 作出不等式组对应的平面区域，利用数形结合进行求解即可．

解答 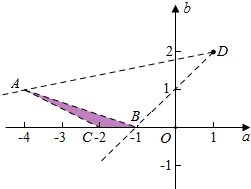解：作出不等式组对应的平面区域如图：
$\frac{a-1}{2b-4}$=$\frac{1}{\frac{2b-4}{a-1}}$=$\frac{1}{2•\frac{b-2}{a-1}}$，
设k=$\frac{b-2}{a-1}$，则k的几何意义为区域内的点到定点D（1，2）的斜率，
由图象可知AD的斜率k=$\frac{1-2}{-4-1}$=$\frac{1}{5}$，
BD的斜率k=$\frac{0-2}{-1-1}=1$，
则$\frac{1}{5}$＜k＜1，
则$\frac{2}{5}$＜2k＜2，$\frac{1}{2}$＜$\frac{1}{2k}$＜$\frac{5}{2}$，
即$\frac{a-1}{2b-4}$的取值范围是（$\frac{1}{2}$，$\frac{5}{2}$），
故答案为：（$\frac{1}{2}$，$\frac{5}{2}$）

点评 本题主要考查线性规划的应用，根据分式的特点，转化为直线斜率的关系是解决本题的关键．