题目内容
2.若a,b∈R,且ab>0,则下列不等式中错误的是①②③(填序号)①a2+b2>2ab;②a+b$≥2\sqrt{ab}$;③$\frac{1}{a}+\frac{1}{b}>\frac{2}{\sqrt{ab}}$;④$\frac{b}{a}$$+\frac{a}{b}$≥2.
分析 根据基本不等式,逐一分析四个不等式的正误,综合讨论结果,可得答案.
解答 解:由a2+b2-2ab=(a-b)2≥0,可得a2+b2≥2ab,当且仅当a=b时取等号,故①错误;
当a<0,b<0时,-a>0,-b>0,此时(-a)+(-b)$≥2\sqrt{ab}$,即a+b$≤-2\sqrt{ab}$,故②错误;
当a<0,b<0时,-a>0,-b>0,此时$\frac{-1}{a}+\frac{-1}{b}≥\frac{2}{\sqrt{ab}}$,即$\frac{1}{a}+\frac{1}{b}≤-\frac{2}{\sqrt{ab}}$,故③错误;
$\frac{b}{a}$$+\frac{a}{b}$≥2$\sqrt{\frac{b}{a}•\frac{a}{b}}$=2,故④正确,
故错误的是:①②③,
故答案为:①②③
点评 本题考查的知识点是基本不等式,难度不大,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
12.若极坐标方程ρ=ρ(θ)满足ρ(θ)=ρ(π-θ),则方程ρ=ρ(θ)表示的图形关于( )
| A. | 极轴对称 | B. | 极点对称 | C. | 射线θ=$\frac{π}{2}$对称 | D. | 不能确定 |
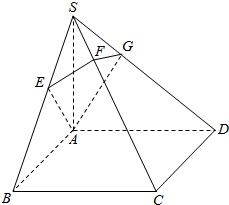 求如图,SA⊥平面ABCD,ABCD是正方形,SC⊥平面AEFG.求证:
求如图,SA⊥平面ABCD,ABCD是正方形,SC⊥平面AEFG.求证: