题目内容
【题目】如图是将一正方体货物沿坡面AB装进汽车货厢的平面示意图.已知长方体货厢的高度BC为 ![]() 米,tanA=
米,tanA= ![]() ,现把图中的货物继续往前平移,当货物顶点D与C重合时,仍可把货物放平装进货厢,求BD的长.(结果保留根号)
,现把图中的货物继续往前平移,当货物顶点D与C重合时,仍可把货物放平装进货厢,求BD的长.(结果保留根号)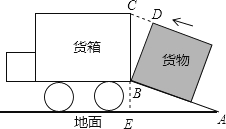
【答案】解:如图,点D与点C重合时,B′C=BD,∠B′CB=∠CBD=∠A,
∵tanA= ![]() ,
,
∴tan∠BCB′= ![]() =
= ![]() ,
,
∴设B′B=x,则B′C=3x,
在Rt△B′CB中,
B′B2+B′C2=BC2 ,
即:x2+(3x)2=( ![]() )2 ,
)2 ,
x= ![]() (负值舍去),
(负值舍去),
∴BD=B′C= ![]() ,
,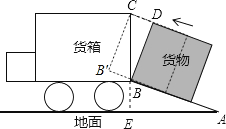
【解析】点D与点C重合时,B′C=BD,∠B′CB=∠CBD=∠A,利用tanA= ![]() 得到tan∠BCB′=
得到tan∠BCB′= ![]() =
= ![]() ,然后设B′B=x,则B′C=3x,在Rt△B′CB中,利用勾股定理求得答案即可.本题考查了解直角三角形的应用,解题的关键是能够从实际问题中整理出直角三角形,难度不大.
,然后设B′B=x,则B′C=3x,在Rt△B′CB中,利用勾股定理求得答案即可.本题考查了解直角三角形的应用,解题的关键是能够从实际问题中整理出直角三角形,难度不大.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目