题目内容
【题目】阿波罗尼斯（约公元前
年）证明过这样一个命题:平面内到两定点距离之比为常数
的点的轨迹是圆，后人将这个圆称为阿波罗尼斯圆.若平面内两定点
、
间的距离为
，动点
满足
，则
的最小值为（ ）
A. 
B. 
C. 
D. 
【答案】A
【解析】
以经过
、
的直线为
轴，线段
的垂直平分线
轴，建立直角坐标系，得出点、的坐标，设点
，利用两点间的距离公式结合条件
得出点
的轨迹方程，然后利用坐标法计算出
的表达式，再利用数形结合思想可求出的最小值.
以经过、的直线为轴，线段的垂直平分线轴，建立直角坐标系，
则
、
，设，
，
，
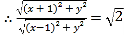两边平方并整理得
，
所以点的轨迹是以
为圆心，
为半径的圆，
则有
，如下图所示：
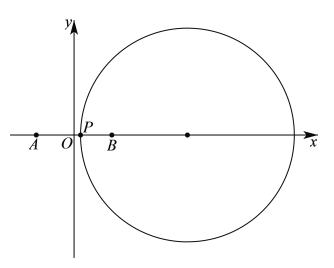
当点为圆与轴的交点（靠近原点）时，此时，
取最小值，且
，
因此，
，故选：A.
练习册系列答案
相关题目
