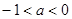题目内容
(12分)(1)设x、y、z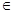 R,且x+y+z=1,求证x2+y2+z2≥
R,且x+y+z=1,求证x2+y2+z2≥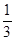 ;
;
(2)设二次函数f (x)=ax2+bx+c(a>0),方程f (x)-x=0有两个实根x1,x2,
且满足:0<x1<x2<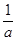 ,若x
,若x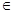 (0,x1)。
(0,x1)。
求证:x<f (x)<x1
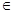 R,且x+y+z=1,求证x2+y2+z2≥
R,且x+y+z=1,求证x2+y2+z2≥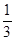 ;
;(2)设二次函数f (x)=ax2+bx+c(a>0),方程f (x)-x=0有两个实根x1,x2,
且满足:0<x1<x2<
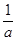 ,若x
,若x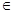 (0,x1)。
(0,x1)。求证:x<f (x)<x1
见解析。
本试题主要是考查了均值不等式的运用以及二次函数中根与系数的关系的综合运用。
(1)x+y+z=1,∴1=(x+y+z)2=x2+y2+z2+2xy+2xz+2yz
≤3(x2+y2+z2)
从而得证。
(2)令F(x)=f(x)-x,x1,x2是f(x)-x=0的根,
∴F(x)=a(x-x1)(x-x2)
∵0<x<x1<x2<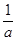 ∴x-x1<0,x-x2<0 a>0
∴x-x1<0,x-x2<0 a>0
∴F(x)>0 即x<f (x)
x1-f (x)=x1-[x+F(x)]=x1-x-a(x-x1)(x-x2)=(x1-x)[1+a(x-x2)]
∵0<x<x1<x2<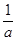
∴x1-x>0 1+a(x-x2)=1+a x-ax2>1-ax2>0
∴x1-f(x)>0 ∴f(x)<x1
综上可知成立。
解:(1)∵x+y+z=1,∴1=(x+y+z)2=x2+y2+z2+2xy+2xz+2yz
≤3(x2+y2+z2)
∴x2+y2+z2≥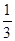
(2)令F(x)=f(x)-x,x1,x2是f(x)-x=0的根,
∴F(x)=a(x-x1)(x-x2)
∵0<x<x1<x2<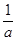 ∴x-x1<0,x-x2<0 a>0
∴x-x1<0,x-x2<0 a>0
∴F(x)>0 即x<f (x)
另一方面:x1-f (x)=x1-[x+F(x)]=x1-x-a(x-x1)(x-x2)=(x1-x)[1+a(x-x2)]
∵0<x<x1<x2<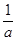
∴x1-x>0 1+a(x-x2)=1+a x-ax2>1-ax2>0
∴x1-f(x)>0 ∴f(x)<x1
综上可得:x<f(x)<x1
(1)x+y+z=1,∴1=(x+y+z)2=x2+y2+z2+2xy+2xz+2yz
≤3(x2+y2+z2)
从而得证。
(2)令F(x)=f(x)-x,x1,x2是f(x)-x=0的根,
∴F(x)=a(x-x1)(x-x2)
∵0<x<x1<x2<
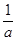 ∴x-x1<0,x-x2<0 a>0
∴x-x1<0,x-x2<0 a>0∴F(x)>0 即x<f (x)
x1-f (x)=x1-[x+F(x)]=x1-x-a(x-x1)(x-x2)=(x1-x)[1+a(x-x2)]
∵0<x<x1<x2<
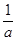
∴x1-x>0 1+a(x-x2)=1+a x-ax2>1-ax2>0
∴x1-f(x)>0 ∴f(x)<x1
综上可知成立。
解:(1)∵x+y+z=1,∴1=(x+y+z)2=x2+y2+z2+2xy+2xz+2yz
≤3(x2+y2+z2)
∴x2+y2+z2≥
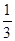
(2)令F(x)=f(x)-x,x1,x2是f(x)-x=0的根,
∴F(x)=a(x-x1)(x-x2)
∵0<x<x1<x2<
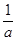 ∴x-x1<0,x-x2<0 a>0
∴x-x1<0,x-x2<0 a>0∴F(x)>0 即x<f (x)
另一方面:x1-f (x)=x1-[x+F(x)]=x1-x-a(x-x1)(x-x2)=(x1-x)[1+a(x-x2)]
∵0<x<x1<x2<
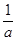
∴x1-x>0 1+a(x-x2)=1+a x-ax2>1-ax2>0
∴x1-f(x)>0 ∴f(x)<x1
综上可得:x<f(x)<x1

练习册系列答案
相关题目
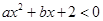 的解集为
的解集为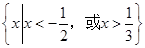 ,则
,则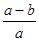 的值为( )
的值为( )

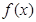 满足条件
满足条件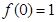 ,及
,及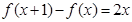 .
.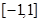 上的最值.
上的最值.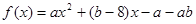 ,当
,当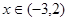 时,
时,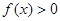 ;
;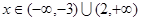 时,
时,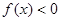
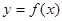 的解析式.
的解析式.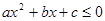 的解集为R.
的解集为R.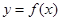 的图像经过坐标原点,其导函数为
的图像经过坐标原点,其导函数为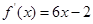 ,数列
,数列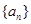 的前n项和为
的前n项和为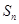 ,点
,点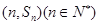 均在函数
均在函数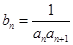 ,
,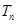 是数列
是数列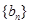 的前n项和,求使得
的前n项和,求使得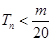 对所有
对所有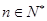 都成立的最小正整数m;
都成立的最小正整数m; 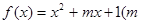 为整数)且关于
为整数)且关于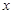 的方程
的方程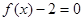 在区间
在区间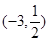 内有两个不同的实根,(1)求整数
内有两个不同的实根,(1)求整数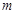 的值;(2)若
的值;(2)若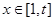 时,总有
时,总有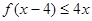 ,求
,求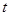 的最大值。
的最大值。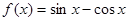 ;②
;②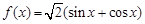 ;③
;③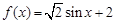 ;④
;④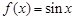 .则其中属于“互为生成函数”的是____________
.则其中属于“互为生成函数”的是____________ 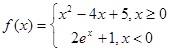 ,若存在不同的实数
,若存在不同的实数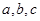 使得
使得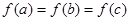 ,则
,则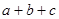 的取值范围是
的取值范围是 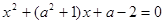 ,有一个根比
,有一个根比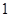 大,另一个根比
大,另一个根比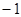 小,则
小,则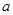 的取值范围是( )
的取值范围是( )