题目内容
已知f(x)=x+
的图象经过点A(3,7),则f(x)的值域为 .
| a |
| x-2 |
考点:函数的最值及其几何意义
专题:函数的性质及应用,不等式的解法及应用
分析:将A(3,7)代入f(x)求得a,可得f(x)=x+
,然后求定义域,在定义域内讨论值域,分类讨论,利用基本不等式求解.
| 4 |
| x-2 |
解答:
解:f(x)=x+
的图象经过点A(3,7),则有3+
=7,解得a=4,
所以f(x)=x+
,定义域为{x|x≠2},
则当x>2时,x-2>0,f(x)=x+
=x-2+
+2≥2
+2=6(当x=4时取得最小值),
当x<2时,x-2<0,f(x)=x+
=x-2+
+2,
此时,-(x-2)>0,x-2+
=-[-(x-2)-
]≤-4,
所以x-2+
+2≤-2,即f(x)≤-2,
则函数值域为(-∞,-2)∪(6,+∞).
故答案为:(-∞,-2)∪(6,+∞).
| a |
| x-2 |
| a |
| 3-2 |
所以f(x)=x+
| 4 |
| x-2 |
则当x>2时,x-2>0,f(x)=x+
| 4 |
| x-2 |
| 4 |
| x-2 |
(x-2)×
|
当x<2时,x-2<0,f(x)=x+
| 4 |
| x-2 |
| 4 |
| x-2 |
此时,-(x-2)>0,x-2+
| 4 |
| x-2 |
| 4 |
| x-2 |
所以x-2+
| 4 |
| x-2 |
则函数值域为(-∞,-2)∪(6,+∞).
故答案为:(-∞,-2)∪(6,+∞).
点评:本题考查函数的值域,利用基本不等式求解,注意不等式的使用条件,凑条件使用公式.

练习册系列答案
相关题目
已知正实数a,b满足a+2b=1,则
的最小值为( )
| b+a |
| ab |
A、3+2
| ||
B、1+
| ||
| C、4 | ||
D、2
|
定义[x]表示不超过x的最大整数,若f(x)=cos(x-[x]),则下列结论中:
①y=f(x)为偶函数;
②y=f(x)为周期函数,周期为2π;
③y=f(x)的最小值为cos1,无最大值;
④y=f(x)无最小值,最大值为1.
正确的命题的个数为( )
①y=f(x)为偶函数;
②y=f(x)为周期函数,周期为2π;
③y=f(x)的最小值为cos1,无最大值;
④y=f(x)无最小值,最大值为1.
正确的命题的个数为( )
| A、0个 | B、1个 | C、3个 | D、4个 |
设a,b,c为正数,a+b+9c2=1,则
+
+
c的最大值是( )
| a |
| b |
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
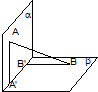 平面α⊥平面β,A∈α,B∈β,AB与两平面α、β所成的角分别为
平面α⊥平面β,A∈α,B∈β,AB与两平面α、β所成的角分别为