题目内容
17.下列函数既是奇函数,又在区间[-1,1]上单调递减的是( )| A. | f(x)=sinx | B. | f(x)=ln$\frac{2-x}{2+x}$ | C. | f(x)=-|x+1| | D. | f(x)=$\frac{1}{2}({e^x}-{e^{-x}})$ |
分析 根据正弦函数的单调性,函数导数符号和函数单调性的关系,奇函数的定义,减函数的定义即可判断每个选项的正误,从而得到正确选项.
解答 解:A.f(x)=sinx在[-1,1]上单调递增;
B.f(x)=$ln\frac{2-x}{2+x}$,解$\frac{2-x}{2+x}>0$得该函数的定义域为[-2,2];
又f′(x)=$\frac{-4}{(2-x)(2+x)}<0$;
∴f(x)在区间[-1,1]上是减函数;
又f(-x)=$ln\frac{2+x}{2-x}=-ln\frac{2-x}{2+x}$=-f(x);
∴f(x)是奇函数;
∴该选项正确;
C.f(x)=-|x+1|,奇函数f(x)在原点有定义时f(0)=0;
而这里f(0)=-1;
∴该函数不是奇函数;
D.$f(x)=\frac{1}{2}({e}^{x}-{e}^{-x})$,f(-1)=$\frac{1}{2}(\frac{1}{e}-e)<\frac{1}{2}(e-\frac{1}{e})=f(1)$;
∴该函数在[-1,1]上不是减函数.
故选B.
点评 考查正弦函数的单调性,函数导数符号和函数单调性的关系,以及奇函数的定义,奇函数f(x)在原点有定义时f(0)=0,减函数的定义.

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
7.已知数列{an}的前n项和为Sn,且a1=1,an+1=2Sn+1(n∈N*),在等差数列{bn}中,b2=5,且公差d=2.使得a1b1+a2b2+…+anbn>60n成立的最小正整数n为( )
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
2.由直线x=$\frac{1}{2}$,x=2,曲线y=-$\frac{1}{x}$及x轴所围图形的面积为( )
| A. | -2ln2 | B. | 2ln2 | C. | $\frac{1}{2}ln2$ | D. | $\frac{15}{4}$ |
17.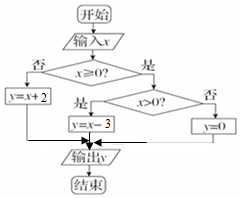 执行如图所示的程序框图,若从集合A={x|-10≤x≤10}中随机取一个数输入,则输出的y值落在区间(-5,2)内的概率是( )
执行如图所示的程序框图,若从集合A={x|-10≤x≤10}中随机取一个数输入,则输出的y值落在区间(-5,2)内的概率是( )
 执行如图所示的程序框图,若从集合A={x|-10≤x≤10}中随机取一个数输入,则输出的y值落在区间(-5,2)内的概率是( )
执行如图所示的程序框图,若从集合A={x|-10≤x≤10}中随机取一个数输入,则输出的y值落在区间(-5,2)内的概率是( )| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
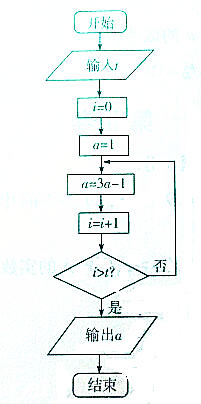 如图是一个程序框图,若输出a的值为365,则输入的t的值可以为5.
如图是一个程序框图,若输出a的值为365,则输入的t的值可以为5.