题目内容
给出下列四个命题:
①函数f(x)=lnx-2+x在区间(1 , e)上存在零点;
②若m≥-1,则函数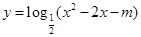 的值域为R;
的值域为R;
③若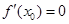 ,则函数y=f(x)在x=x0处取得极值;
,则函数y=f(x)在x=x0处取得极值;
④“a =1”是“函数 在定义域上是奇函数”的充分不必要条件。
在定义域上是奇函数”的充分不必要条件。
其中正确的是 。
【答案】
①②④
【解析】
试题分析:由f(x)=lnx-2+x得: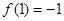 ,
,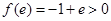 ,所以
,所以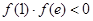 ,则函数在区间(1 , e)上存在零点,①正确;若m≥-1,满足
,则函数在区间(1 , e)上存在零点,①正确;若m≥-1,满足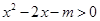 ,所以函数
,所以函数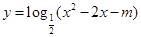 的值域为R,②正确;若
的值域为R,②正确;若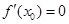 ,当
,当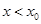
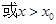 时,
时,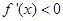 ,则函数y=f(x)在x=x0处没有取得极值,③错误;当
,则函数y=f(x)在x=x0处没有取得极值,③错误;当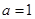 时,
时,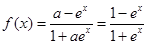 ,则满足
,则满足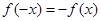 ,故函数
,故函数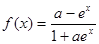 在定义域上是奇函数,另外,由
在定义域上是奇函数,另外,由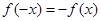 解得
解得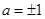 ,所以“a =1”是“函数
,所以“a =1”是“函数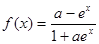 在定义域上是奇函数”的充分不必要条件,④正确,故①②④正确。
在定义域上是奇函数”的充分不必要条件,④正确,故①②④正确。
考点:命题的真假性
点评:判断命题的真假性是一个考点,这种题目涉及知识点多,因而比较难,所以可用到排除法。

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目