题目内容
抛物线P:x2=2py上一点Q(m,2)到抛物线P的焦点的距离为3,A、B、C、D为抛物线的四个不同的点,其中A、D关于y轴对称,D(x0,y0),B(x1,y1),C(x2,y2),-x0<x1<x0<x2,直线BC平行于抛物线P的以D为切点的切线.(1)求p的值;
(2)证明:∠BAC的角平分线在直线AD上;
(3)D到直线AB、AC的距离分别为m、n,且m+n=
| 2 |
分析:(1)由|QF|=3=2+
,能求出p.
(2)由抛物线方程为x2=4y,知A(-x0,
),D(x0,
),B(x1,
),C(x2,
),由y′=
,知KBC=
=
=
,由此能推导出∠BAC的角平分线在直线AD上.
(3)设∠BAD=∠CAD=α,则m=n=|AD|sinα,sinα=
.由此能推导出直线BC的方程.
| p |
| 2 |
(2)由抛物线方程为x2=4y,知A(-x0,
| ||
| 4 |
| ||
| 4 |
| ||
| 4 |
| ||
| 4 |
| x |
| 2 |
| ||||||||
| x1-x2 |
| x1+x2 |
| 4 |
| x0 |
| 2 |
(3)设∠BAD=∠CAD=α,则m=n=|AD|sinα,sinα=
| ||
| 2 |
解答:解:(1)∵|QF|=3=2+
∴p=2(2分)
(2)∴抛物线方程为x2=4y
A(-x0,
),D(x0,
),B(x1,
),C(x2,
)∵y′=
∴KBC=
=
=
∴x1+x2=2x0∵KAC=
=
KAB=
=
∴KAC+KAB=
+
=
=0
所以直线AC和直线AB的倾斜角互补,所以∠BAD=∠CAD∴∠BAC的角平分线在直线AD上(6分)
(3)设∠BAD=∠CAD=α
则m=n=|AD|sinα∴sinα=
,∵α∈(0.
)∴α=
∴lAC:y-
=x+x0即y=x+
+x0
把lAC:y=x+
+x0与抛物线方程x2=4y联立的x2-4x-4x0-x02=0∴-x0x2=-4x0-x02∴x2=x0+4
同理可得x1=x0-4∵-x0<x0-4<x0∴x0>2∴S△ABC=
|AB||AC|=
(4+2x0)
(2x0-4)=4(
-4)=48
∴x0=4(10分)∴B(0,0)∴lBC:y=2x(12分)
| p |
| 2 |
(2)∴抛物线方程为x2=4y
A(-x0,
| ||
| 4 |
| ||
| 4 |
| ||
| 4 |
| ||
| 4 |
| x |
| 2 |
∴KBC=
| ||||||||
| x1-x2 |
| x1+x2 |
| 4 |
| x0 |
| 2 |
| ||||||||
| x2+x0 |
| x2-x0 |
| 4 |
| ||||||||
| x1+x0 |
| x1-x0 |
| 4 |
∴KAC+KAB=
| x2-x0 |
| 4 |
| x1-x 0 |
| 4 |
| x 1+x2-2x0 |
| 4 |
所以直线AC和直线AB的倾斜角互补,所以∠BAD=∠CAD∴∠BAC的角平分线在直线AD上(6分)
(3)设∠BAD=∠CAD=α
则m=n=|AD|sinα∴sinα=
| ||
| 2 |
| π |
| 2 |
| π |
| 4 |
| ||
| 4 |
| ||
| 4 |
把lAC:y=x+
| ||
| 4 |
同理可得x1=x0-4∵-x0<x0-4<x0∴x0>2∴S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 2 |
| x | 2 0 |
∴x0=4(10分)∴B(0,0)∴lBC:y=2x(12分)
点评:本题考查直线和圆锥曲线的位置关系,解题时要认真审题,注意挖掘题设中的隐含条件,合理地进行等价转化.

练习册系列答案
相关题目
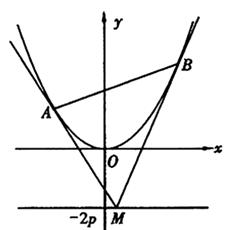
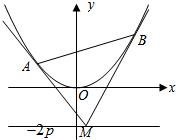 如图,设抛物线方程为x2=2py(p>0),M为直线y=-2p上任意一点,过M引抛物线的切线,切点分别为A,B.
如图,设抛物线方程为x2=2py(p>0),M为直线y=-2p上任意一点,过M引抛物线的切线,切点分别为A,B. 如图,设抛物线方程为x2=2py(p>0),M为直线y=-2p上任意一点,过M引抛物线的切线,切点分别为A,B.
如图,设抛物线方程为x2=2py(p>0),M为直线y=-2p上任意一点,过M引抛物线的切线,切点分别为A,B.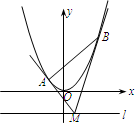 如图,设抛物线方程为x2=2py(p>0),M为直线l:y=-2p上任意一点,过M引抛物线的切线,切点分别为A、B.
如图,设抛物线方程为x2=2py(p>0),M为直线l:y=-2p上任意一点,过M引抛物线的切线,切点分别为A、B.