题目内容
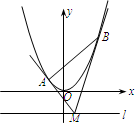 如图,设抛物线方程为x2=2py(p>0),M为直线l:y=-2p上任意一点,过M引抛物线的切线,切点分别为A、B.
如图,设抛物线方程为x2=2py(p>0),M为直线l:y=-2p上任意一点,过M引抛物线的切线,切点分别为A、B.(1)设抛物线上一点P到直线l的距离为d,F为焦点,当d-|PF|=
| 3 | 2 |
(2)若M(2,-2),求线段AB的长;
(3)求M到直线AB的距离的最小值.
分析:(1)根据d-|PF|=
,得yP+2p-(yP+
)=
=
,由此可求抛物线方程;
(2)求出抛物线方程与过M点的直线为y=k(x-2)-2联立,利用直线与抛物线相切,可求得xB-xA=4
,xB+xA=4.根据A、B在抛物线上,可求yB-yA,从而可求线段AB的长;
(3)设M(m,-2p),过M点的直线与抛物线联立,利用直线与抛物线相切,可得x1-x2=p(k1-k2),y1-y2=
=
=
,从而可得直线AB的方程,利用点到直线的距离公式求得点M到AB的距离,利用基本不等式,即可求M到直线AB的距离的最小值.
| 3 |
| 2 |
| p |
| 2 |
| 3p |
| 2 |
| 3 |
| 2 |
(2)求出抛物线方程与过M点的直线为y=k(x-2)-2联立,利用直线与抛物线相切,可求得xB-xA=4
| 2 |
(3)设M(m,-2p),过M点的直线与抛物线联立,利用直线与抛物线相切,可得x1-x2=p(k1-k2),y1-y2=
| ||||
| 2p |
| (x1-x2)(x1+x2) |
| 2p |
| p2(k1-k2)(k1+k2) |
| 2p |
解答:解:(1)由d-|PF|=
,得yP+2p-(yP+
)=
=
,∴p=1,
∴抛物线方程为x2=2y.
(2)M(2,-2)在直线y=-2p上,∴-2=-2p,解得p=1,
∴抛物线方程为x2=2y,
设过M点的直线为y=k(x-2)-2,联立:
,消去y,得
=kx-2k-2
即x2-2kx+4(k+1)=0(*),
∵直线与抛物线相切,∴△=0,即4k2-16(k+1)=0
∴k2-4k-4=0,∴k=2±2
,此时,方程(*)有等根x=k,
∴xB=2+2
,xA=2-2
,
∴xB-xA=4
,xB+xA=4.
∵A、B在抛物线上,
∴yB-yA=
=
=8
∴|AB|=
=
=4
.
(3)设M(m,-2p),过M点的直线为L:y=k(x-m)-2p,联立:
,消去y,得
=kx-km-2p,
∴x2-2kpx+2p(km+2p)=0①,
∵直线与抛物线相切,∴△=0
∴4k2p2-8p(km+2p)=0,∴pk2-2mk-4p=0②,此时方程①有等根x=kp,
令A(x1,y1),B(x2,y2),则x1-x2=p(k1-k2),y1-y2=
=
=
,
∴AB的斜率k′=
=
,
由②,根据韦达定理可得k1+k2=
,∴k′=
,
∴直线AB的方程为y-y1=
(x-x1),
∴y-
=
(x-k1p)
∴化简可得2py-
p2=2mx-2mk1p,
∴2mx-2py+p(p
-2mk1)=0,
由②pk2-2mk-4p=0,∴p
-2mk1=4p,
∴AB方程化为:2mx-2py+4p2=0,
∴点M到AB的距离d=
=
=
=
+
≥2
=2
p,
当且仅当
=
,即m2+p2=3p2,
∴m=±
p时,上式等号成立,
∴M到直线AB的距离的最小值为2
p.
| 3 |
| 2 |
| p |
| 2 |
| 3p |
| 2 |
| 3 |
| 2 |
∴抛物线方程为x2=2y.
(2)M(2,-2)在直线y=-2p上,∴-2=-2p,解得p=1,
∴抛物线方程为x2=2y,
设过M点的直线为y=k(x-2)-2,联立:
|
| x2 |
| 2 |
即x2-2kx+4(k+1)=0(*),
∵直线与抛物线相切,∴△=0,即4k2-16(k+1)=0
∴k2-4k-4=0,∴k=2±2
| 2 |
∴xB=2+2
| 2 |
| 2 |
∴xB-xA=4
| 2 |
∵A、B在抛物线上,
∴yB-yA=
| ||||
| 2 |
| (xB+xA)(xB-xA) |
| 2 |
| 2 |
∴|AB|=
| (xB-xA)2+(yB-yA)2 |
| 32+128 |
| 10 |
(3)设M(m,-2p),过M点的直线为L:y=k(x-m)-2p,联立:
|
| x2 |
| 2p |
∴x2-2kpx+2p(km+2p)=0①,
∵直线与抛物线相切,∴△=0
∴4k2p2-8p(km+2p)=0,∴pk2-2mk-4p=0②,此时方程①有等根x=kp,
令A(x1,y1),B(x2,y2),则x1-x2=p(k1-k2),y1-y2=
| ||||
| 2p |
| (x1-x2)(x1+x2) |
| 2p |
| p2(k1-k2)(k1+k2) |
| 2p |
∴AB的斜率k′=
| y1-y2 |
| x1-x2 |
| k1+k2 |
| 2 |
由②,根据韦达定理可得k1+k2=
| 2m |
| p |
| m |
| p |
∴直线AB的方程为y-y1=
| m |
| p |
∴y-
| ||
| 2p |
| m |
| p |
∴化简可得2py-
| k | 2 1 |
∴2mx-2py+p(p
| k | 2 1 |
由②pk2-2mk-4p=0,∴p
| k | 2 1 |
∴AB方程化为:2mx-2py+4p2=0,
∴点M到AB的距离d=
| |2m•m-2p(-2p)+4p2| | ||
|
| |2m2+8p2| | ||
|
| (m2+p2)+3p2 | ||
|
| m2+p2 |
| 3p2 | ||
|
| 3p2 |
| 3 |
当且仅当
| m2+p2 |
| 3p2 | ||
|
∴m=±
| 2 |
∴M到直线AB的距离的最小值为2
| 3 |
点评:本题考查抛物线的标准方程,考查直线与抛物线的位置关系,考查点到直线的距离公式,考查基本不等式的运用,综合性强.

练习册系列答案
相关题目
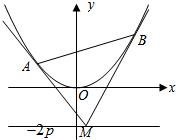 如图,设抛物线方程为x2=2py(p>0),M为直线y=-2p上任意一点,过M引抛物线的切线,切点分别为A,B.
如图,设抛物线方程为x2=2py(p>0),M为直线y=-2p上任意一点,过M引抛物线的切线,切点分别为A,B. 如图,设抛物线方程为x2=2py(p>0),M为直线y=-2p上任意一点,过M引抛物线的切线,切点分别为A,B.
如图,设抛物线方程为x2=2py(p>0),M为直线y=-2p上任意一点,过M引抛物线的切线,切点分别为A,B. ,
,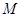 为直线
为直线 上任意一点,过
上任意一点,过 .
.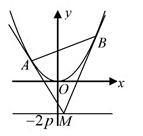
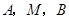 三点的横坐标成等差数列;
三点的横坐标成等差数列;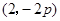 时,
时,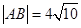 .求此时抛物线的方程。
.求此时抛物线的方程。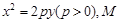 直线
直线 上任意一点,过M引抛物线的切线,切点分别为A,B。
上任意一点,过M引抛物线的切线,切点分别为A,B。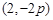 时,
时,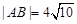 ,求此时抛物线的方程;
,求此时抛物线的方程; 上,其中,点C满足
上,其中,点C满足 (O为坐标原点).若存在,求出所有适合题意的点M的坐标;若不存在,请说明理由.
(O为坐标原点).若存在,求出所有适合题意的点M的坐标;若不存在,请说明理由.